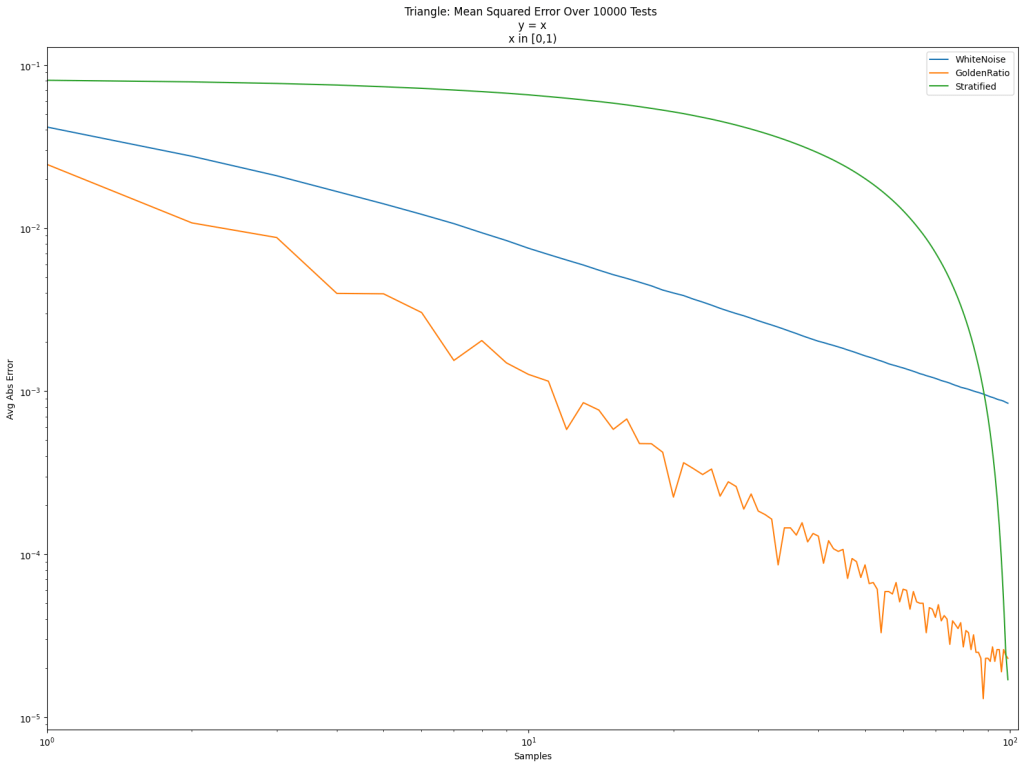
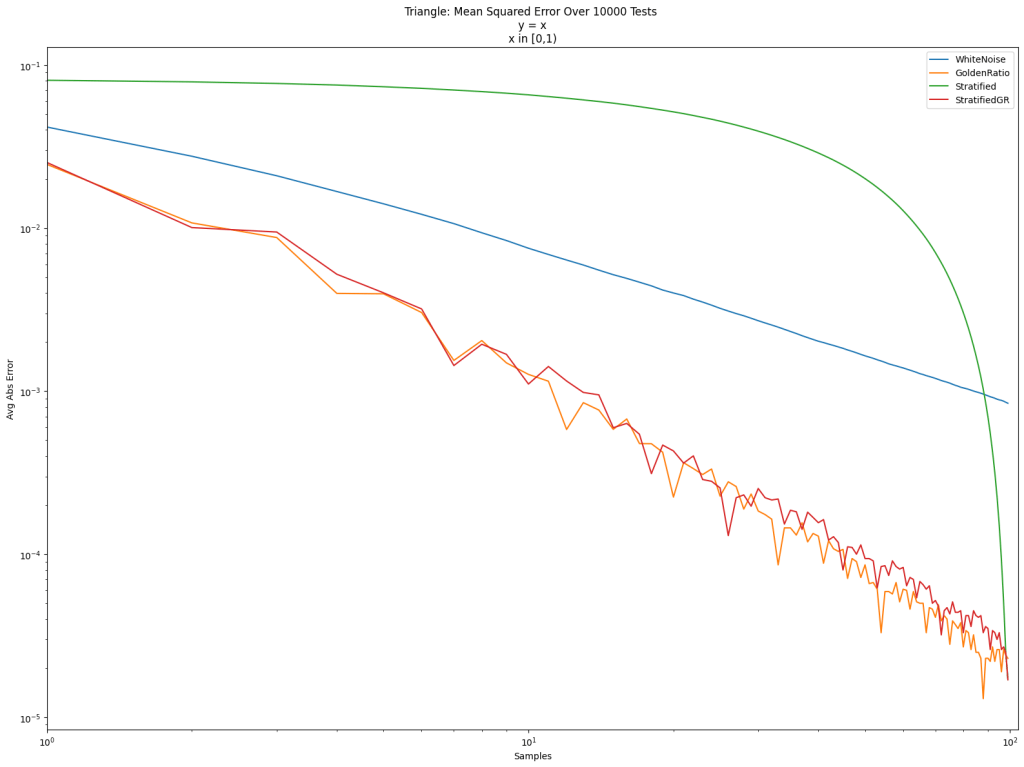
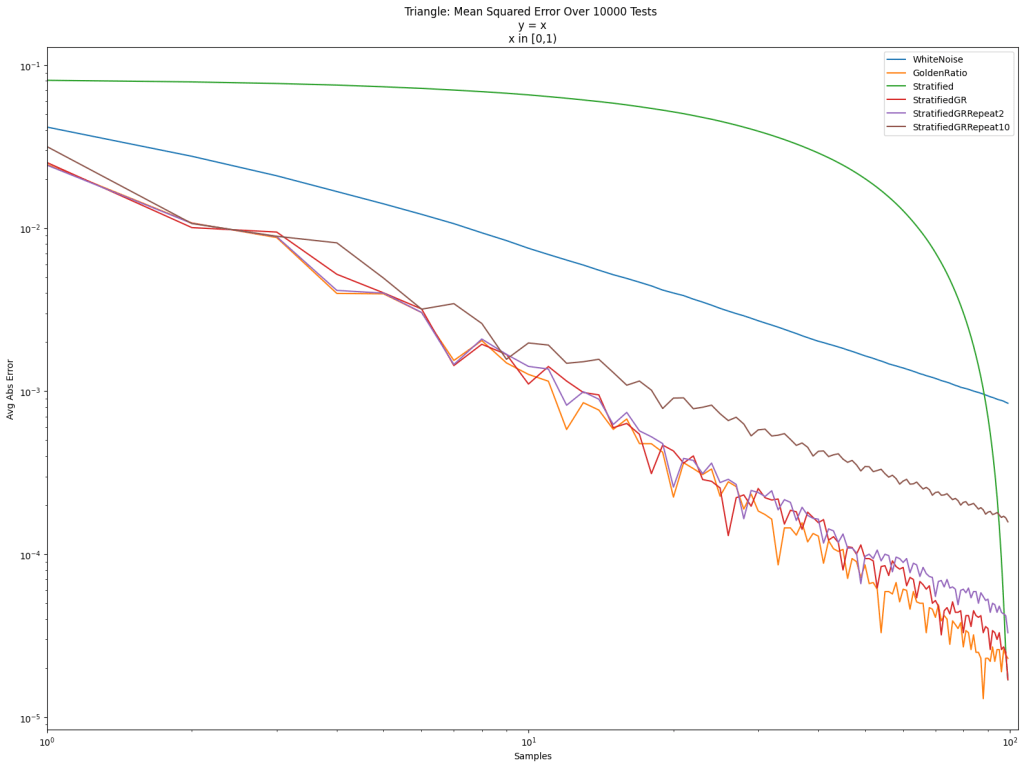
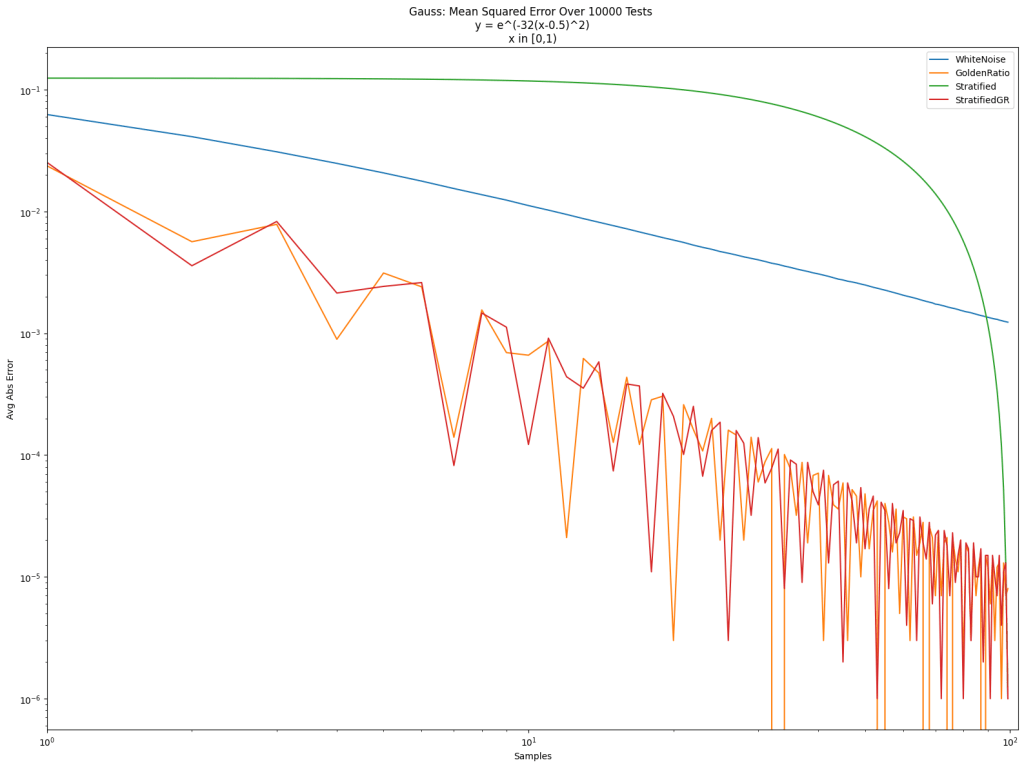
Derivatives, Gradients, Jacobians and Hessians – Oh My!

This article explains how these four things fit together and shows some examples of what they are used for.

Derivatives

Derivatives are the most fundamental concept in calculus. If you have a function, a derivative tells you how much that function changes at each point.

If we start with the function $y=x^2-6x+13$ , we can calculate the derivative as $y'=2x-6$ . Here are those two functions graphed.

One use of derivatives is for optimization – also known as finding the lowest part on a graph.

If you were at $x = 1$ and wanted to know whether you should go left or right to get lower, the derivative can tell you. Plugging 1 into $2x-6$ gives the value -4. A negative derivative means taking a step to the right will make the y value go down, so going right is down hill. We could take a step to the right and check the derivative again to see if we’ve walked far enough. As we are taking steps, if the derivative becomes positive, that means we went too far and need to turn around, and start going left. If we shrink our step size whenever we go too far in either direction, we can get arbitrarily close to the actual minimum point on the graph.

What I just described is an iterative optimization method that is similar to gradient descent. Gradient descent simulates a ball rolling down hill to find the lowest point that we can, adjusting step size, and even adding momentum to try and not get stuck in places that are not the true minimum.

We can make an observation though: The minimum of a function is flat, and has a derivative of 0. If not, that would mean it was on a hill, which means that going either left or right is lower, so it wouldn’t be the minimum.

Armed with this knowledge, another way to use derivatives to find the minimum is to find where the derivative is 0. We can do that by solving the equation $2x-6 = 0$ and getting the value $x=3$ . Without iteration, we found that the minimum of the function is at $x=3$ and we can plug 3 into the original equation $y=x^2-6x+13$ to find out that the minimum y value is 4.

Things get more complicated when the functions are higher order than quadratic. Higher order functions have both minimums and maximums, and both of those have 0 derivatives. Also, if the $x^2$ term of a quadratic is negative, then it only has a maximum, instead of a minimum.

Higher dimensional functions also get more complex, where for instance you could have a point on a two dimensional function $z=f(x,y)$ that is a local minimum for x but a local maximum for y. The gradient will be zero in each direction, despite it not being a minimum, and the simulated ball will get stuck.

Gradients

Speaking of higher dimensional functions, that is where gradients come in.

If you have a function $w=f(x,y,z)$ , a gradient is a vector of derivatives, where you consider changing only one variable at a time, leaving the other variables constant. The notation for a gradient looks like this:

$\nabla f(x,y,z) = \begin{bmatrix} \frac{\partial w}{\partial x} & \frac{\partial w}{\partial y} & \frac{\partial w}{\partial z} \end{bmatrix}$

Looking at a single entry in the vector, $\frac{\partial w}{\partial x}$ , that means “The derivative of w with respect to x”. Another way of saying that is “If you added 1 to x before plugging it into the function, this is how much w would change, if the function was a straight line”. These are called partial derivatives, because they are derivatives of one variable, in a function that takes multiple variables.

Let’s work through calculating the gradient of the function $w=3x^2+6yz^3+4$ .

To calculate the derivative of w with regard to x ( $\frac{\partial w}{\partial x}$ ), we take the derivative of the function as usual, but we only treat x as a variable, and all other variables as constants. That gives us with $6x$ .

Calculating the derivative of w with regard to y, we treat y as a variable and all others as constants to get: $6z^3$ .

Lastly, to calculate the derivative of w with regard to z, we treat z as a variable and all others as constants. That gives us $18yz^2$ .

The full gradient of the function is: $\begin{bmatrix} 6x & 6z^3 & 18yz^2 \end{bmatrix}$ .

An interesting thing about gradients is that when you calculate them for a specific point, they give a vector that points in the direction of the biggest increase in the function, or equivalently, in the steepest uphill direction. The opposite direction of the gradient is the biggest decrease of the function, or the steepest downhill direction. This is why gradients are used in the optimization method “Gradient Descent”. The gradient (multiplied by a step size) is subtracted from a point to move it down hill.

Besides optimization, gradients can also be used in rendering. For instance, here it’s used for rendering anti aliased signed distance fields: https://iquilezles.org/articles/distance/

Jacobian Matrix

Let’s say you had a function that took in multiple values and gave out multiple values: $v,w =f(x,y,z)$ .

We could calculate the gradient of this function for v, and we could calculate it for w. If we put those two gradient vectors together to make a matrix, we would get the Jacobian matrix! You can also think of a gradient vector as being the Jacobian matrix of a function that outputs a single scalar value, instead of a vector.

Here is the Jacobian for $v,w =f(x,y,z)$ :

$\mathbb{J} = \begin{bmatrix} \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} & \frac{\partial v}{\partial z} \\ \frac{\partial w}{\partial x} & \frac{\partial w}{\partial y} & \frac{\partial w}{\partial z} \end{bmatrix}$

If that’s hard to read, the top row is the gradient for v, and the bottom row is the gradient for w.

When you evaluate the Jacobian matrix at a specific point in space (of whatever space the input parameters are in), it tells you how the space is warped in that location – like how much it is rotated and squished. You can also take the determinant of the Jacobian to see if things in that area get bigger (determinant greater than 1), smaller (determinant less than 1 but greater than 0), or if they get flipped inside out (determinant is negative). If the determinant is zero, it means it squishes everything into a single point (or line, etc. at least one dimension is scaled to 0), and also means that the operation can’t be reversed (the matrix can’t be inverted).

Here’s a great 10 minute video that goes into Jacobian Matrices a little more deeply and shows how they can be useful in machine learning: https://www.youtube.com/watch?v=AdV5w8CY3pw

Since Jacobians describe warping of space, they are also useful in computer graphics, where for instance, you might want to use alpha transparency to fade an object out over a specific number of pixels to perform anti aliasing, but the object may be described in polar coordinates, or be warped in way that makes it hard to know how many units to fade out over in that modified space. This has come up for me when doing 2D SDF rendering in shadertoy.

Hessian Matrix

If you take all partial derivatives (aka make a gradient) of a function $w=f(x,y,z)$ , that will give you a vector with three partial derivatives out – one for x, one for y, one for z.

What if we wanted to get the 2nd derivatives? In other words, what if we wanted to take the derivative of the derivatives?

You could just take the derivative with respect to the same variables again, but to really understand the second derivatives of the function, we should take all three partial derivatives (one for x, one for y, one for z) of EACH of those three derivatives in the gradient.

That would give us 9 derivatives total, and that is exactly what the Hessian Matrix is.

$\mathbb{H} = \begin{bmatrix} \frac{\partial^2 w}{\partial x^2} & \frac{\partial^2 w}{\partial xy} & \frac{\partial^2 w}{\partial xz} \\ \frac{\partial^2 w}{\partial yx} & \frac{\partial^2 w}{\partial y^2} & \frac{\partial^2 w}{\partial yz} \\ \frac{\partial^2 w}{\partial zx} & \frac{\partial^2 w}{\partial zy} & \frac{\partial^2 w}{\partial z^2} \end{bmatrix}$

If that is hard to read, each row is the gradient, but then the top row is differentiated with respect to x, the middle row is differentiated with respect to y, and the bottom row is differentiated with respect to z.

Another way to think about the Hessian is that it’s the transpose of the Jacobian matrix of the gradient. That’s a mouthful, but it hopefully helps you better see how these things fit together.

Taking the 2nd derivative of a function tells you how the function curves, which can be useful (again!) for optimization.

This 11 minute video talks about how the Hessian is used in optimization to get the answer faster, by knowing the curvature of the functions: https://www.youtube.com/watch?v=W7S94pq5Xuo

Where a derivative approximates a function locally with a line, a second order derivative approximates a function locally with a quadratic. So, a Hessian can let you model a function at a point as a quadratic type of function, and then do the neat trick from the derivative section of going straight to the minimum instead of having to iterate. That takes you to the minimum of the quadratic, not the minimum of the function you are trying to optimize, but that can be a great speed up for certain types of functions. You can also use the eigenvalues of the Hessian to know if it’s positive definite – aka if it’s a parabola pointing upwards and so actually has a minimum – vs if it’s pointing downwards, or is a saddle point. The eigenvectors can tell you the orientation of the paraboloid as well. Here is more information on analyzing a Hessian matrix: https://web.stanford.edu/group/sisl/k12/optimization/MO-unit4-pdfs/4.10applicationsofhessians.pdf

Calculating the Hessian can be quite costly both computationally and in regards to how much memory it uses, for machine learning problems that have millions of parameters or more. In those cases, there are quasi newton methods, which you can watch an 11 minute video about here: https://www.youtube.com/watch?v=UvGQRAA8Yms

Thanks for reading and hopefully this helps clear up some scary sounding words!

Toroidally Progressive Stratified Sampling in 1D

The code that made the diagrams in this post can be found at https://github.com/Atrix256/ToroidalProgressiveStratification1D

I stumbled on this when working on something else. I’m not sure of a use case for it, but I want to share it in case there is one I’m not thinking of, or in case it inspires other ideas.

Let’s say you want to do Monte Carlo integration on a function y=f(x) for x being between 0 and 10. You can do this by choosing random values for x between 0 and 10, and averaging the y values to get an “average height” of the function between those two points. This leaves you with a rectangle where you know the width (10) and you are estimating the height (the average y value). You just multiply the width by that estimated height to get an estimate of the integral. The more points you use, the more accurate your estimate is. You can use Monte Carlo integration to solve integrals that you can’t solve analytically.

For deeper information Monte Carlo integration including importance sampling, give this a read: https://blog.demofox.org/2018/06/12/monte-carlo-integration-explanation-in-1d/

We use Monte Carlo integration A LOT in rendering, and specifically real time rendering. This is especially true in the modern age of ray traced rendering. When a render is noisy, what you are seeing is the error from Monte Carlo integration not being accurate enough with the number of samples we can afford computationally. We then try to fix the noise using various methods, such as filtering and denoising, or by changing how we pick the x values to plug in (better sampling patterns). Here are some relevant resources:

When Random Numbers Are Too Random: Low Discrepancy Sequences – https://blog.demofox.org/2017/05/29/when-random-numbers-are-too-random-low-discrepancy-sequences/
“Beyond White Noise for Real-Time Rendering” (YouTube) – https://www.youtube.com/watch?v=tethAU66xaA
“Importance-Sampled Filter-Adapted Spatio-Temporal Sampling” – https://github.com/electronicarts/importance-sampled-FAST-noise

Let’s say we want to integrate the function y=f(x) where x is a scalar value between 0 and 1. Three common ways to do this are:

Uniform White Noise – Use a standard random number generator (or hash function) to generate numbers between 0 and 1.
Golden Ratio – Starting with any value, add the golden ratio to it (1.6180339887…) and throw away the whole numbers (aka take the result mod 1) to get a random value (quasirandom technically). repeat to get more values.
Stratified – If you know you want to take N samples, break the 0 to 1 range into N equally sized bins, and put one uniform white noise value in each bucket. Like if you wanted to take two samples, you’d have a random number between 0 and 1/2, and another between 1/2 and 1. A problem with uniform white noise is that it tends to clump up and leave big holes. Stratification helps make the points more evenly spaced.

Here’s a log/log error graph using those 3 kinds of sampling strategies to integrate the function y=x from 0 to 1. The x axis is the number of samples, and the y axis is error.

White noise is terrible as usual. Friends don’t let friends use white noise. The golden ratio sequence is great, as per usual. Golden ratio for the win! Stratification is also quite good, but it doesn’t give very good results until the end.

Stratified sampling doesn’t do well in the middle because we are picking points in order. Like for 100 points, we sample between 0 and 1/100, then between 1/100 and 2/100, then between 2/100 and 3/100 and so on. By the end it fills in the space between 0 and 1, but it takes a while to get there.

The question is… can we make stratified sampling that is good all along the way, instead of only being good at the end? The answer is yes we can.

An observation is that we could visit those bins in a different order. But what order should we visit them in? We are going to get a bit meta and visit them in “golden ratio” order. If are taking N samples, we are going to pretend that N is 1.0, and we are going to do golden ratio sampling to pick the order of the buckets to do stratified sampling in. If we naively used the golden ratio sequence, multiplied by N and cast to integer to get the bucket index, we’d find we hit some of the buckets multiple times, and missed some of the buckets. But it turns out that we can find an integer coprime to N that is closest to the golden ratio. We can then start at any index, and repeatedly add that number to our index to get the next index – making sure to take the result modulo N. We will then visit each bucket exactly once before repeating the sequence.

That’s a brief description of a low discrepancy shuffle iterator I wrote up on a previous blog post: https://blog.demofox.org/2024/05/19/a-low-discrepancy-shuffle-iterator-random-access-inversion/.

Doing that, we get “StratifiedGR” below. It does nearly as well as the golden ratio sequence, but the final result is the same as if we did stratification in order.

Is this useful? Well, it’s hard to tell in general whether stratified sampling or golden ratio wins for taking N samples in Monte Carlo integration.

The golden ratio (orange) is usually lower error than the golden ratio shuffled stratifed sampling (red), but the ending error is 0.000017 for “StratifedGR” (same as Stratified), while it is 0.000023 for “GoldenRatio” (and 0.000843 for “WhiteNoise”), so stratification has lower error in the end.

A nice thing about the golden ratio sequence is that you can always add more points to the sequence, where for stratified sampling – and even golden ratio shuffled stratified sampling – you have to know the number of samples you want to take in advance and can’t naturally extend it and add more.

Stratifed sampling is randomized within the buckets, so we could repeat the sequence again to get new samples, but we are using the same buckets, and we are putting white noise values in them, so our sequence just sort of gets “white noise gains”, instead of the gains that a progressive, open, low discrepancy sequence gives. Below we repeat golden ratio shuffled stratification twice (purple) and 10 times (brown). You can see that golden ratio shuffled stratification loses quality when you repeat it. You really need to know how many samples you want at max, when doing golden ratio shuffled stratified sampling, but you are free to use less than than number.

By doing a golden ratio shuffle on stratified sampling, we did make it progressive (“good” at any number of samples), but we also made it progressive from any index (“good” starting from any index, for any number of samples). That is a pretty neat property, and comes from the fact that our golden ratio shuffle iterator is actually a rank 1 lattice, just like the actual golden ratio sequence, and this is a property of all rank 1 lattices.

However, by golden ratio shuffling stratification, we also made it TOROIDALLY progressive. What i mean by that is that the sampling sequence is finite, but that you can start at any index and have “good” sampling for any number of samples EVEN WHEN THE SEQUENCE FINISHES AND STARTS OVER. There is no “seam” when this sequence starts over. It just keeps going at the full level of quality. This is due to the fact that our “golden ratio shuffle iterator” rank 1 lattice uses a number that is coprime to N to visit all the indicies [0, N) exactly once before repeating.

This torodial progressiveness is useful if you have a lot of things doing integration at once, all using the same sampling sequence for the function, but individually, they may be (re)starting integration on different time intervals. That may sound strange and exotic, but that is exactly what is happening in temporal anti aliasing (TAA). We have a global sub pixel camera jitter, which is the x we plug into the y=f(x) as we integrate every pixel over its footprint, but each pixel individually uses neighborhood color clamping and other heuristics to decide when it should throw out the integration history and start over.

The only challenge is that if we wanted to use something like this for TAA, we would need a 2D sequence for the camera jitter instead of 1D. I do happen to have a blog post on a 2D version of the low discrepancy shuffler. I don’t think that will magically be the answer needed here, but perhaps you can smell what I’m cooking 😛

A Two Dimensional Low Discrepancy Shuffle Iterator (+Random Access & Inversion): https://blog.demofox.org/2024/10/04/a-two-dimensional-low-discrepancy-shuffle-iterator-random-access-inversion/

I should note there are other ways to do progressive stratified sampling, for instance the great 2018 paper “Progressive Multi-Jittered Sample Sequences” by Per Christensen, Andrew Kensler and Charlie Kilpatrick. https://graphics.pixar.com/library/ProgressiveMultiJitteredSampling/paper.pdf

In the post so far, we’ve only looked at integrating the “triangle” function y=x. Below are the results for that again, and also for a step function, a sine function, and a Gaussian function. Different sampling sequences behave better or worse with different types of integrands sometimes.

Final Error Amounts:

	Gauss	Sine	Step	Triangle
WhiteNoise	0.001232	0.002671	0.002425	0.000843
GoldenRatio	0.000008	0.000024	0.000052	0.000023
Stratified	0.000001	0.000011	0.000033	0.000017
StratifiedGR	0.000001	0.000011	0.000033	0.000017