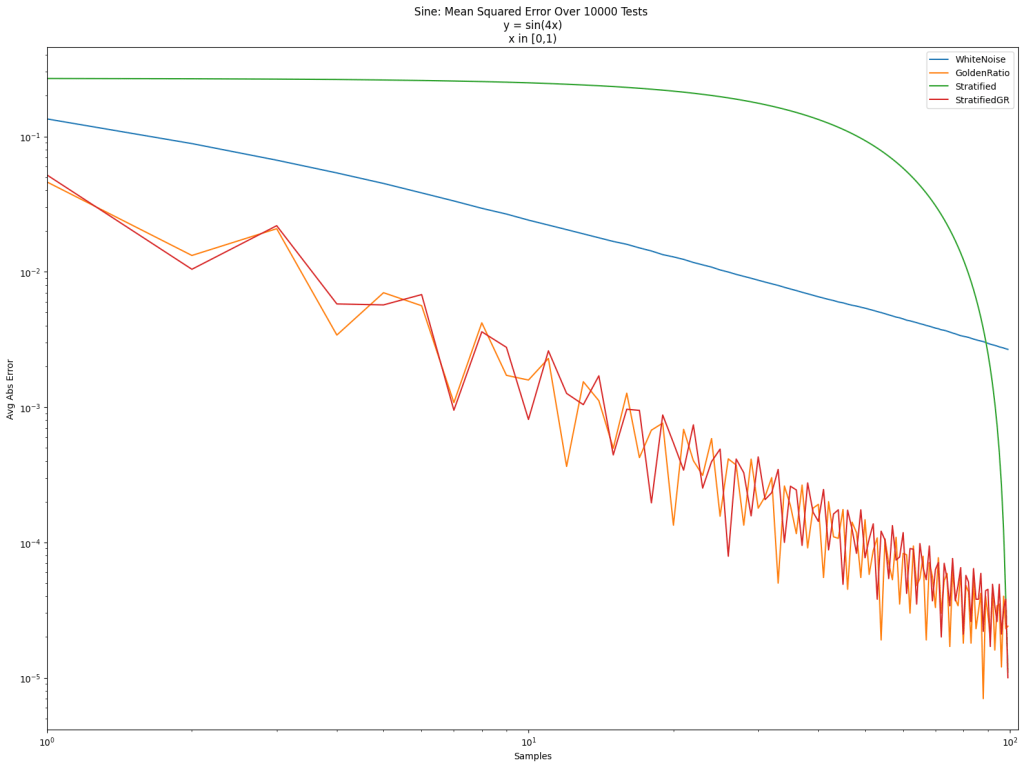
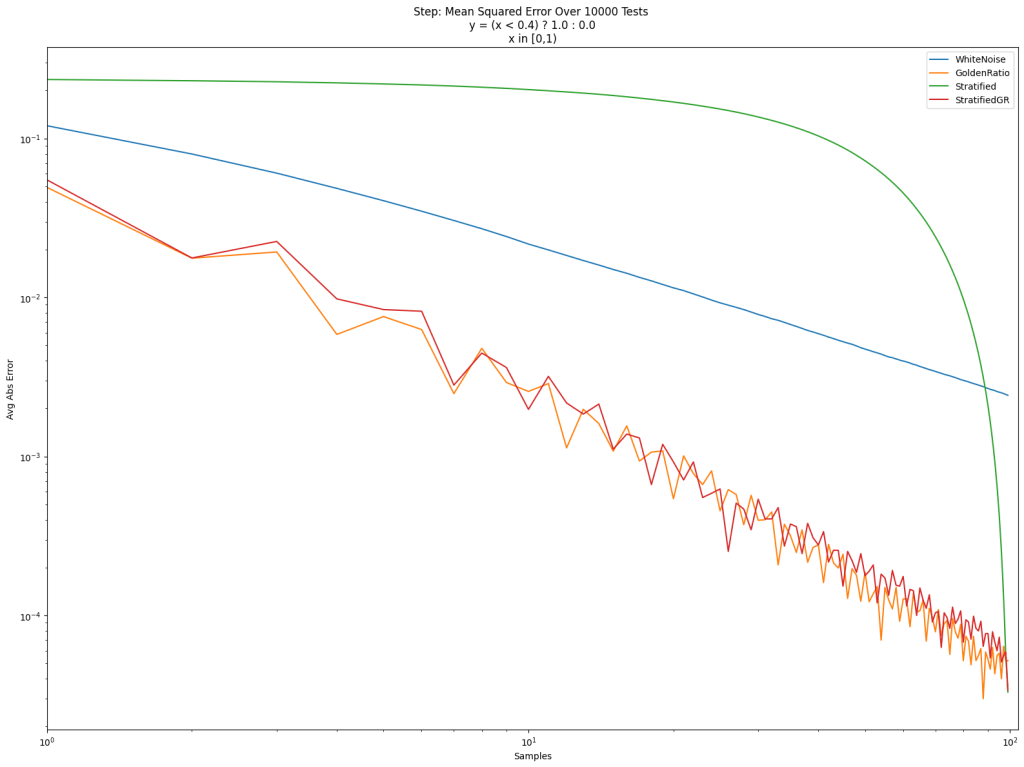
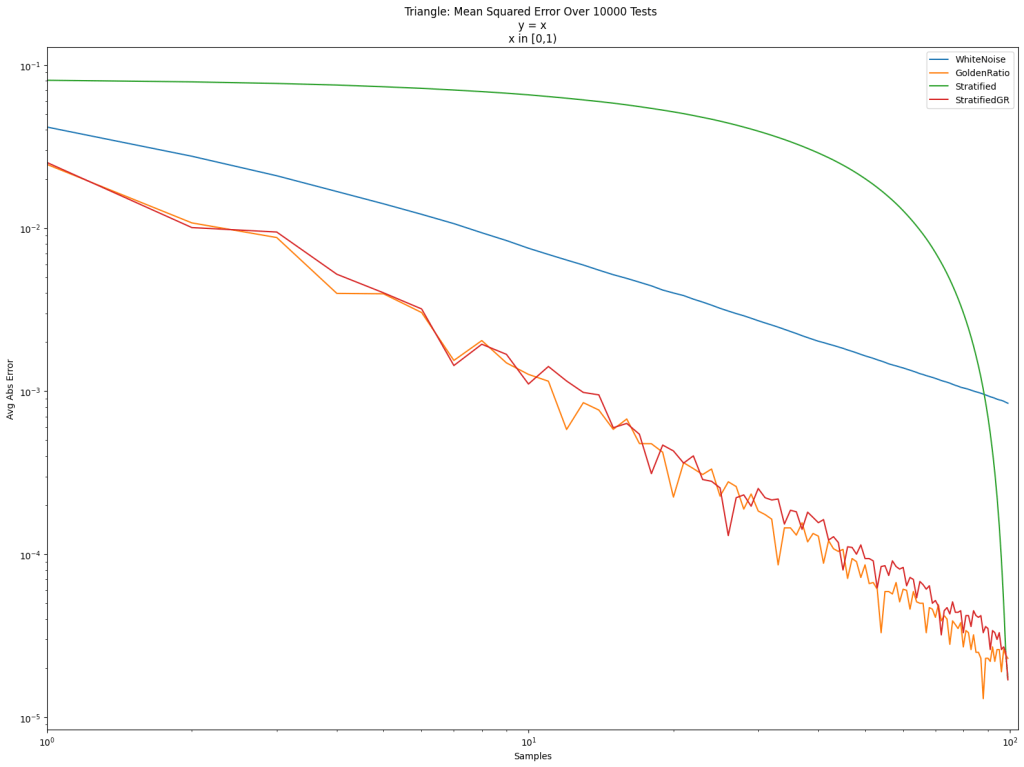
Using Information Entropy To Make Choices / Choose Experiments

I recently watched a great 16 minute YouTube video on the basics of information theory: https://www.youtube.com/watch?v=bkLHszLlH34.

The video shows the link between probability and information entropy and a great takeaway from it is that you can use these concepts to decide what kind of experiments to do, to get as much information as possible. This could be useful if you are limited by time, computation, chemicals, or other resources. It seems like you could also mix this with “Fractional Factorial Experiment Design” somehow (https://blog.demofox.org/2023/10/17/fractional-factorial-experiment-design-when-there-are-too-many-experiments-to-do/).

Probability and Bits

Information theory links probability to bits of information using this formula:

$\text{b}=\log_2{\frac{1}{p}}$

where p is the probability of an event happening, and b is the number of bits generated by that event.

Using a fair coin as an example, there is a 50% (1/2) chance of heads and a 50% (1/2) chance of tails. In both cases, p=0.5. Let’s calculate how many bits flipping a head gives us:

$b = \log_2{\frac{2}{1}} = 1$

So flipping a coin and getting heads would give us 1 bit, and so would getting tails, since it has the same probability. This makes some perverse sense, since we can literally generate random bits by flipping a coin and using Heads / Tails as 0 / 1.

What if we had a weighted coin that had a 75% (3/4) chance of heads, and a 25% (3/4) chance of tails?

$b_{\text{heads}} = \log_2{\frac{4}{3}} = 0.415$

$b_{\text{tails}} = \log_2{\frac{4}{1}} = 2$

So, flipping a heads gives us only 0.415 bits of information, but flipping tails gives us 2 bits of information. When something is lower probability, it’s more surprising when it happens, and it gives us more bits.

What if we had a two headed coin so that flipping heads was a 100% (1/1) chance, and tails was a 0% (0/1) chance?

$b_{\text{heads}} = \log_2{\frac{1}{1}} = 0$

$b_{\text{tails}} = \log_2{\frac{1}{0}} = \text{undefined}$

The math says that flipping a 2 headed coin is a deterministic result and gives us no bits of information!

Submarine Game

The submarine game is a simplified and single player version of battleship where you have a grid of MxN cells, and one of the cells contains a submarine. The game is to guess a cell to attack, and it’s revealed whether the submarine was there or not. The game ends when the submarine is found.

At each step in the game, if there are U cells which are covered, there is a 1/U chance of shooting the submarine and a (U-1)/U chance of missing the submarine.

You can think of this a different way: The goal is to find the position of the submarine, and if you miss the submarine, you eliminate one of the possibilities, giving you some more information about where the submarine is by showing you where it isn’t and narrowing down the search. If you hit the submarine, you get all remaining information and the game ends.

If you had a 4×4 grid, there are 16 different places the submarine could be in, so you could store the position in 4 bits. Every time you miss the submarine, you gain a fraction of those bits. When you eventually hit the submarine you gain the remaining fraction of those bits!

Let’s see this in action with a smaller 4×1 grid. With only 4 cells, the submarine position can be encoded with 2 bits, so 2 bits is the total amount of information we are trying to get.

Turn 1

On the first turn we can choose from 4 cells to reveal. 3 cells are empty, and 1 cell is the submarine, so we have a 75% (3/4) chance of missing the submarine, and a 25% (1/4) chance of hitting it. Lets calculate how many bits of information each would give us:

$b_{\text{miss}} = \log_2{\frac{4}{3}} = 0.415$

$b_{\text{hit}} = \log_2{\frac{4}{1}} = 2$

This shows that if we find the submarine, we gain the full 2 bits of information all at once. Otherwise, we gain 0.415 bits of information.

Turn 2

Miss

If we got to the second turn, we missed on the first turn and have accumulated 0.415 bits of information. There are 3 cells to reveal. 2 cells are empty and 1 has the submarine. There is a 66% (2/3) chance to miss the submarine, and a 33% (1/3) chance to hit the submarine.

$b_{\text{miss}} = \log_2{\frac{3}{2}} = 0.585$

$b_{\text{hit}} = \log_2{\frac{3}{1}} = 1.585$

If we hit the submarine, we get 1.585 bits of information to add to the 0.415 bits of information we got in the first turn, which adds together to give us the full 2 bits of information needed to locate the submarine. Otherwise, we gain 0.585 more bits of information giving us 0.415+0.585=1 bits of info total, and continue on to turn 3.

Turn 3

Miss

On turn 3 there are 2 cells to reveal. 1 cell is empty and 1 has the submarine, so there is a 50% (1/2) chance for either missing or hitting the submarine. We also have accumulated 1 bit of information, which makes sense because we’ve eliminated half of the cells and have half the number of bits we need.

$b_{\text{miss}} = \log_2{\frac{2}{1}} = 1$

$b_{\text{hit}} = \log_2{\frac{2}{1}} = 1$

If we hit the submarine, it gives us the other bit we need, and if we miss the submarine, it also gives us the other bit we need. Either we hit the submarine and know where it is, or we revealed the final cell that doesn’t have the submarine in it, so we know the submarine is in the final unrevealed cell.

If we missed, let’s continue onto Turn 4, even though we have accumulated 2 bits of information already.

Turn 4

Miss

On turn 4 there is 1 cell to reveal. 0 cells are empty and 1 has the submarine, so there is a 100% (1/1) chance to hit the submarine, and 0% (0/1) chance to miss. We also already have 2 bits of information accumulated from the previous rounds, while only needing 2 bits of information total to know where the submarine is.

$b_{\text{miss}} = \log_2{\frac{1}{0}} = undefined$

$b_{\text{hit}} = \log_2{\frac{1}{1}} = 0$

The math tells us that we got no new information from revealing the final cell. It was completely deterministic and we knew the outcome already. Turn 4 was not necessary.

Neat, isn’t it?

Miss

Hit

Expected Information Entropy

Besides being able to calculate the number of bits we’d get from a possible result, we can also look at all possibilities of an event simultaneously and get an expected number of bits to get from the event. You calculate this by calculating the bits for each possible event, multiplying by the probability, and summing them all up.

Fair Coin

Going back to the coin example, with a fair coin, there is a 50% (1/2) chance of landing heads, and a 50% (1/2) chance of being tails. Let’s calculate the number of bits that gives us again:

$b_{\text{heads}} = \log_2{\frac{2}{1}} = 1$

$b_{\text{tails}} = \log_2{\frac{2}{1}} = 1$

We then multiply them each by their probability of coming up and add them together. That is a weighted of the number of bits the events generate, weighted by their probability of happening.

$\mathbb{E}(b) = b_{\text{heads}} * p_{\text{heads}} + b_{\text{tails}} * p_{\text{tails}}$

$\mathbb{E}(b) = 1 * 0.5 + 1 * 0.5$

$\mathbb{E}(b) = 1$

So, the expected number of bits generated from a fair coin flip is 1 bit.

I’m using the notion $\mathbb{E}(b)$ to mean expected information entropy, but in other sources you’ll commonly see it as $H(X)$ where $X$ is the event, and $x_i$ are the outcomes.

Unfair (Biased) Coin

How about the unfair coin that had a 75% (3/4) chance of heads, and a 25% (3/4) chance of tails?

$b_{\text{heads}} = \log_2{\frac{4}{3}} = 0.415$

$b_{\text{tails}} = \log_2{\frac{4}{1}} = 2$

Now let’s multiply each by their probability and add them together:

$\mathbb{E}(b) = b_{\text{heads}} * p_{\text{heads}} + b_{\text{tails}} * p_{\text{tails}}$

$\mathbb{E}(b) = 0.415 * 3/4 + 2 * 1/4$

$\mathbb{E}(b) = 0.811$

The biased coin gave us less information on average than the fair coin. The fair coin gave 1 bit, while this unfair coin only gave 0.811 bits. Interesting!

Fair Coin + Edge (Unfair 3 Sided Coin)

Let’s run the numbers for a coin where there’s a 49% chance to land heads, a 49% chance to land tails, and a 2% chance to land edge on.

$b_{\text{heads}} = \log_2{\frac{1}{0.49}} = 1.029$

$b_{\text{tails}} = \log_2{\frac{1}{0.49}} = 1.029$

$b_{\text{edge}} = \log_2{\frac{1}{0.02}} = 5.644$

Now let’s calculate the expected information entropy:

$\mathbb{E}(b) = b_{\text{heads}} * p_{\text{heads}} + b_{\text{tails}} * p_{\text{tails}} + b_{\text{edge}} * p_{\text{edge}}$

$\mathbb{E}(b) = 1.029 * 0.49 + 1.029 * 0.49 + 5.644 * 0.02$

$\mathbb{E}(b) = 1.121$

Equal Chance For Heads, Tails, Edge (Fair 3 Sided Coin)

Lastly, let’s do the math for a coin that has equal chances of landing heads, tails, or edge. All of them being a 33% (1/3) chance.

$b_{\text{heads}} = \log_2{\frac{1}{0.33}} = 1.585$

Tails and edge have the same probability so same number of bits. If we take the weighted average of that, since they are all the same, we get:

$\mathbb{E}(b) = 1.585$

It looks to me that the expected bits are highest when the probabilities are equal. I asked Claude who said that is true, and gave a proof I could follow, as well as an intuitive explanation.

Using Expected Information Entropy To Choose Experiments

The video has a neat question they use “Expected Information Entropy” to solve:

Imagine you have 12 balls. 11 of them weigh the same, but 1 ball is either heavier or lighter than the others. You have a scale to help you figure out which ball is the “odd ball”. What is your strategy for finding it using the least number of weighings as possible?

Tangent: My 11 year old son Loki said the answer was 2 if you get lucky. Put one ball on each side of the scale, and if one of them is the odd ball, the scale will show an uneven weight. Replace one of the balls with another ball from the pile. If the scale goes flat, the ball that was removed was the “odd ball”, else it’s the ball that did not get removed. This answer relies on luck, but it is the minimum number of weighings possible.

For the “real” solution, the video wants you to instead think about the lowest number of EXPECTED weighings.

For the first weighing you have to decide how many balls to put on the left and right side of the scale.

We actually know that there are 3 possible outcomes of this are:

The left side of the scale goes down.
The right side of the scale goes down.
The scale is level.

If we decide how many balls to put on each side, we can calculate the probabilities of the outcomes.

1 Ball Each Side

For 1 ball on each side:

The left side of the scale goes down. 1/12 chance.
The right side of the scale goes down. Also a 1/12 chance.
The scale is level. a 10/12 chance.

If it doesn’t make sense to you how I came up with these probabilities, the next section explains it.

Since we know the outcomes and their probabilities, we can calculate the expected entropy information!

$b_{\text{left}} = b_{\text{right}} = \log2{\frac{12}{1}} = 3.585$

$b_{\text{flat}} = \log2{\frac{12}{10}} = 0.263$

$\mathbb{E}(b) = 3.585 * 1 / 12 + 3.585 * 1 / 12 + 0.263 * 10 / 12 = 0.817$

Putting 1 ball on each side for the first weighing gives us 0.817 bits of information on average.

2 Balls Each Side

The left side goes down: 2/12 chance
The right side goes down: 2/12 chance
The scale is level: 8/12 chance

$b_{\text{left}} = b_{\text{right}} = \log2{\frac{12}{2}} = 2.585$

$b_{\text{flat}} = \log2{\frac{12}{8}} = 0.585$

$\mathbb{E}(b) = 2.585 * 2 / 12 + 2.585 * 2 / 12 + 0.585 * 8 / 12 = 1.252$

Putting 2 balls on each side gives us 1.252 bits of information on average.

The Rest

We could calculate the rest of them, but I’ll show you the final chart and leave it up to you to calculate them all if you want to!

Balls On Each Side	Expected Information Entropy
1	0.82
2	1.25
3	1.50
4	1.58
5	1.48
6	1.0

As you can see, weighing 4 balls gives the most expected information entropy. On average, it’s the best thing to do for the first weighing. Something interesting is that when you put 4 balls on each side, there are 4 balls left on the table, so it is equal chance that the scale tilts left, lays flat, or tilts right. Just like we saw at the end of the last section, having 3 options with equally probable events gives the most expected information entropy.

A good heuristic to take away from all of this seems to be that if you are trying to decide what kind of measurement or experiment to do next, you should do whichever one has as close to even probabilities of all outcomes as possible.

I feel like this must relate to dimensionality reduction (like PCA or SVD), where you find a lower dimensional projection that has the most variance.

The video explains what to do after you do the first ball weighing, but it essentially comes down to calculating the expected information entropy for the next set of outcomes, and choosing the highest one. It turns out you can isolate the ball with 3 weighings total, when you work this way.

Bonus: Calculating Odds Of Scale Results

This is what makes sense to me. Your mileage may vary.

Let’s say we have 3 balls and label them A,B,C. A is the odd ball and is heavier than B and C. There are 6 ways to arrange these letters.
ABC
ACB
BAC
BCA
CAB
CBA

If we take the left letter of the strings above to be what is on the left side of the scale, the middle letter means what is on the right side of the scale, and the right letter means what is left on the table, we have our 6 possible ball configurations.

Out of those configurations, 2 out of 6 have A on the left of the scale, so the scale tilts to the left. 2 of the 6 have A on the right of the scale, so the scale tilts to the right. The last 2 of the 6 have A on the table, so the scale is flat. If A was light instead of heavy, you just reverse the tilt left and tilt right but everything else stays the same.

In the problem asked, there are 12 balls though, which are a lot more letters. In general, for N letters representing N balls, there are N! ways to arrange those letters. Each letter appears in each position an equal number of times, which is (N-1)! ways. So, the percentage of the time a letter is in a specific column is (N-1)! / (N!), or 1/N. Another way to get here is to just realize that every column has every letter in it the same number of times, so with N letters, each letter appears in the column 1/N percent of the time.

For 1 ball on each side, for our 3 cases we just count:

Tilt Left: The percentage of times the oddball “A” is in the first column (1/12).
Tilt Right: The percentage of times the oddball “A” is in the second column (1/12).
Flat: The remainder to make the percentages add up to 1 (12/12 – 1/12 – 1/12 = 10/12).

So for 12 balls, it’s 1/12 for each of the tilt directions, leaving 10/12 as the remainder, for the odd ball to be on the table.

For 2 balls on each side, we count:

Tilt Left: The percentage of times the oddball “A” is in the first column or second column (1/12 + 1/12 = 2/12).
Tilt Right: The percentage of times the oddball “A” is in the third column or fourth column (1/12 + 1/12 = 2/12).
Flat: the remainder (12/12 – 2/12 – 2/12 = 8/12).

So, it’s 2/12 for each of the tilt directions, and 8/12 for the remainder.

The pattern continues for higher ball counts being weighed.

Hopefully you found this post interesting. Thanks for reading!

Derivatives, Gradients, Jacobians and Hessians – Oh My!

This article explains how these four things fit together and shows some examples of what they are used for.

Derivatives

Derivatives are the most fundamental concept in calculus. If you have a function, a derivative tells you how much that function changes at each point.

If we start with the function $y=x^2-6x+13$ , we can calculate the derivative as $y'=2x-6$ . Here are those two functions graphed.

One use of derivatives is for optimization – also known as finding the lowest part on a graph.

If you were at $x = 1$ and wanted to know whether you should go left or right to get lower, the derivative can tell you. Plugging 1 into $2x-6$ gives the value -4. A negative derivative means taking a step to the right will make the y value go down, so going right is down hill. We could take a step to the right and check the derivative again to see if we’ve walked far enough. As we are taking steps, if the derivative becomes positive, that means we went too far and need to turn around, and start going left. If we shrink our step size whenever we go too far in either direction, we can get arbitrarily close to the actual minimum point on the graph.

What I just described is an iterative optimization method that is similar to gradient descent. Gradient descent simulates a ball rolling down hill to find the lowest point that we can, adjusting step size, and even adding momentum to try and not get stuck in places that are not the true minimum.

We can make an observation though: The minimum of a function is flat, and has a derivative of 0. If not, that would mean it was on a hill, which means that going either left or right is lower, so it wouldn’t be the minimum.

Armed with this knowledge, another way to use derivatives to find the minimum is to find where the derivative is 0. We can do that by solving the equation $2x-6 = 0$ and getting the value $x=3$ . Without iteration, we found that the minimum of the function is at $x=3$ and we can plug 3 into the original equation $y=x^2-6x+13$ to find out that the minimum y value is 4.

Things get more complicated when the functions are higher order than quadratic. Higher order functions have both minimums and maximums, and both of those have 0 derivatives. Also, if the $x^2$ term of a quadratic is negative, then it only has a maximum, instead of a minimum.

Higher dimensional functions also get more complex, where for instance you could have a point on a two dimensional function $z=f(x,y)$ that is a local minimum for x but a local maximum for y. The gradient will be zero in each direction, despite it not being a minimum, and the simulated ball will get stuck.

Gradients

Speaking of higher dimensional functions, that is where gradients come in.

If you have a function $w=f(x,y,z)$ , a gradient is a vector of derivatives, where you consider changing only one variable at a time, leaving the other variables constant. The notation for a gradient looks like this:

$\nabla f(x,y,z) = \begin{bmatrix} \frac{\partial w}{\partial x} & \frac{\partial w}{\partial y} & \frac{\partial w}{\partial z} \end{bmatrix}$

Looking at a single entry in the vector, $\frac{\partial w}{\partial x}$ , that means “The derivative of w with respect to x”. Another way of saying that is “If you added 1 to x before plugging it into the function, this is how much w would change, if the function was a straight line”. These are called partial derivatives, because they are derivatives of one variable, in a function that takes multiple variables.

Let’s work through calculating the gradient of the function $w=3x^2+6yz^3+4$ .

To calculate the derivative of w with regard to x ( $\frac{\partial w}{\partial x}$ ), we take the derivative of the function as usual, but we only treat x as a variable, and all other variables as constants. That gives us with $6x$ .

Calculating the derivative of w with regard to y, we treat y as a variable and all others as constants to get: $6z^3$ .

Lastly, to calculate the derivative of w with regard to z, we treat z as a variable and all others as constants. That gives us $18yz^2$ .

The full gradient of the function is: $\begin{bmatrix} 6x & 6z^3 & 18yz^2 \end{bmatrix}$ .

An interesting thing about gradients is that when you calculate them for a specific point, they give a vector that points in the direction of the biggest increase in the function, or equivalently, in the steepest uphill direction. The opposite direction of the gradient is the biggest decrease of the function, or the steepest downhill direction. This is why gradients are used in the optimization method “Gradient Descent”. The gradient (multiplied by a step size) is subtracted from a point to move it down hill.

Besides optimization, gradients can also be used in rendering. For instance, here it’s used for rendering anti aliased signed distance fields: https://iquilezles.org/articles/distance/

Jacobian Matrix

Let’s say you had a function that took in multiple values and gave out multiple values: $v,w =f(x,y,z)$ .

We could calculate the gradient of this function for v, and we could calculate it for w. If we put those two gradient vectors together to make a matrix, we would get the Jacobian matrix! You can also think of a gradient vector as being the Jacobian matrix of a function that outputs a single scalar value, instead of a vector.

Here is the Jacobian for $v,w =f(x,y,z)$ :

$\mathbb{J} = \begin{bmatrix} \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} & \frac{\partial v}{\partial z} \\ \frac{\partial w}{\partial x} & \frac{\partial w}{\partial y} & \frac{\partial w}{\partial z} \end{bmatrix}$

If that’s hard to read, the top row is the gradient for v, and the bottom row is the gradient for w.

When you evaluate the Jacobian matrix at a specific point in space (of whatever space the input parameters are in), it tells you how the space is warped in that location – like how much it is rotated and squished. You can also take the determinant of the Jacobian to see if things in that area get bigger (determinant greater than 1), smaller (determinant less than 1 but greater than 0), or if they get flipped inside out (determinant is negative). If the determinant is zero, it means it squishes everything into a single point (or line, etc. at least one dimension is scaled to 0), and also means that the operation can’t be reversed (the matrix can’t be inverted).

Here’s a great 10 minute video that goes into Jacobian Matrices a little more deeply and shows how they can be useful in machine learning: https://www.youtube.com/watch?v=AdV5w8CY3pw

Since Jacobians describe warping of space, they are also useful in computer graphics, where for instance, you might want to use alpha transparency to fade an object out over a specific number of pixels to perform anti aliasing, but the object may be described in polar coordinates, or be warped in way that makes it hard to know how many units to fade out over in that modified space. This has come up for me when doing 2D SDF rendering in shadertoy.

Hessian Matrix

If you take all partial derivatives (aka make a gradient) of a function $w=f(x,y,z)$ , that will give you a vector with three partial derivatives out – one for x, one for y, one for z.

What if we wanted to get the 2nd derivatives? In other words, what if we wanted to take the derivative of the derivatives?

You could just take the derivative with respect to the same variables again, but to really understand the second derivatives of the function, we should take all three partial derivatives (one for x, one for y, one for z) of EACH of those three derivatives in the gradient.

That would give us 9 derivatives total, and that is exactly what the Hessian Matrix is.

$\mathbb{H} = \begin{bmatrix} \frac{\partial^2 w}{\partial x^2} & \frac{\partial^2 w}{\partial xy} & \frac{\partial^2 w}{\partial xz} \\ \frac{\partial^2 w}{\partial yx} & \frac{\partial^2 w}{\partial y^2} & \frac{\partial^2 w}{\partial yz} \\ \frac{\partial^2 w}{\partial zx} & \frac{\partial^2 w}{\partial zy} & \frac{\partial^2 w}{\partial z^2} \end{bmatrix}$

If that is hard to read, each row is the gradient, but then the top row is differentiated with respect to x, the middle row is differentiated with respect to y, and the bottom row is differentiated with respect to z.

Another way to think about the Hessian is that it’s the transpose of the Jacobian matrix of the gradient. That’s a mouthful, but it hopefully helps you better see how these things fit together.

Taking the 2nd derivative of a function tells you how the function curves, which can be useful (again!) for optimization.

This 11 minute video talks about how the Hessian is used in optimization to get the answer faster, by knowing the curvature of the functions: https://www.youtube.com/watch?v=W7S94pq5Xuo

Where a derivative approximates a function locally with a line, a second order derivative approximates a function locally with a quadratic. So, a Hessian can let you model a function at a point as a quadratic type of function, and then do the neat trick from the derivative section of going straight to the minimum instead of having to iterate. That takes you to the minimum of the quadratic, not the minimum of the function you are trying to optimize, but that can be a great speed up for certain types of functions. You can also use the eigenvalues of the Hessian to know if it’s positive definite – aka if it’s a parabola pointing upwards and so actually has a minimum – vs if it’s pointing downwards, or is a saddle point. The eigenvectors can tell you the orientation of the paraboloid as well. Here is more information on analyzing a Hessian matrix: https://web.stanford.edu/group/sisl/k12/optimization/MO-unit4-pdfs/4.10applicationsofhessians.pdf

Calculating the Hessian can be quite costly both computationally and in regards to how much memory it uses, for machine learning problems that have millions of parameters or more. In those cases, there are quasi newton methods, which you can watch an 11 minute video about here: https://www.youtube.com/watch?v=UvGQRAA8Yms

Thanks for reading and hopefully this helps clear up some scary sounding words!

Toroidally Progressive Stratified Sampling in 1D

The code that made the diagrams in this post can be found at https://github.com/Atrix256/ToroidalProgressiveStratification1D

I stumbled on this when working on something else. I’m not sure of a use case for it, but I want to share it in case there is one I’m not thinking of, or in case it inspires other ideas.

Let’s say you want to do Monte Carlo integration on a function y=f(x) for x being between 0 and 10. You can do this by choosing random values for x between 0 and 10, and averaging the y values to get an “average height” of the function between those two points. This leaves you with a rectangle where you know the width (10) and you are estimating the height (the average y value). You just multiply the width by that estimated height to get an estimate of the integral. The more points you use, the more accurate your estimate is. You can use Monte Carlo integration to solve integrals that you can’t solve analytically.

For deeper information Monte Carlo integration including importance sampling, give this a read: https://blog.demofox.org/2018/06/12/monte-carlo-integration-explanation-in-1d/

We use Monte Carlo integration A LOT in rendering, and specifically real time rendering. This is especially true in the modern age of ray traced rendering. When a render is noisy, what you are seeing is the error from Monte Carlo integration not being accurate enough with the number of samples we can afford computationally. We then try to fix the noise using various methods, such as filtering and denoising, or by changing how we pick the x values to plug in (better sampling patterns). Here are some relevant resources:

When Random Numbers Are Too Random: Low Discrepancy Sequences – https://blog.demofox.org/2017/05/29/when-random-numbers-are-too-random-low-discrepancy-sequences/
“Beyond White Noise for Real-Time Rendering” (YouTube) – https://www.youtube.com/watch?v=tethAU66xaA
“Importance-Sampled Filter-Adapted Spatio-Temporal Sampling” – https://github.com/electronicarts/importance-sampled-FAST-noise

Let’s say we want to integrate the function y=f(x) where x is a scalar value between 0 and 1. Three common ways to do this are:

Uniform White Noise – Use a standard random number generator (or hash function) to generate numbers between 0 and 1.
Golden Ratio – Starting with any value, add the golden ratio to it (1.6180339887…) and throw away the whole numbers (aka take the result mod 1) to get a random value (quasirandom technically). repeat to get more values.
Stratified – If you know you want to take N samples, break the 0 to 1 range into N equally sized bins, and put one uniform white noise value in each bucket. Like if you wanted to take two samples, you’d have a random number between 0 and 1/2, and another between 1/2 and 1. A problem with uniform white noise is that it tends to clump up and leave big holes. Stratification helps make the points more evenly spaced.

Here’s a log/log error graph using those 3 kinds of sampling strategies to integrate the function y=x from 0 to 1. The x axis is the number of samples, and the y axis is error.

White noise is terrible as usual. Friends don’t let friends use white noise. The golden ratio sequence is great, as per usual. Golden ratio for the win! Stratification is also quite good, but it doesn’t give very good results until the end.

Stratified sampling doesn’t do well in the middle because we are picking points in order. Like for 100 points, we sample between 0 and 1/100, then between 1/100 and 2/100, then between 2/100 and 3/100 and so on. By the end it fills in the space between 0 and 1, but it takes a while to get there.

The question is… can we make stratified sampling that is good all along the way, instead of only being good at the end? The answer is yes we can.

An observation is that we could visit those bins in a different order. But what order should we visit them in? We are going to get a bit meta and visit them in “golden ratio” order. If are taking N samples, we are going to pretend that N is 1.0, and we are going to do golden ratio sampling to pick the order of the buckets to do stratified sampling in. If we naively used the golden ratio sequence, multiplied by N and cast to integer to get the bucket index, we’d find we hit some of the buckets multiple times, and missed some of the buckets. But it turns out that we can find an integer coprime to N that is closest to the golden ratio. We can then start at any index, and repeatedly add that number to our index to get the next index – making sure to take the result modulo N. We will then visit each bucket exactly once before repeating the sequence.

That’s a brief description of a low discrepancy shuffle iterator I wrote up on a previous blog post: https://blog.demofox.org/2024/05/19/a-low-discrepancy-shuffle-iterator-random-access-inversion/.

Doing that, we get “StratifiedGR” below. It does nearly as well as the golden ratio sequence, but the final result is the same as if we did stratification in order.

Is this useful? Well, it’s hard to tell in general whether stratified sampling or golden ratio wins for taking N samples in Monte Carlo integration.

The golden ratio (orange) is usually lower error than the golden ratio shuffled stratifed sampling (red), but the ending error is 0.000017 for “StratifedGR” (same as Stratified), while it is 0.000023 for “GoldenRatio” (and 0.000843 for “WhiteNoise”), so stratification has lower error in the end.

A nice thing about the golden ratio sequence is that you can always add more points to the sequence, where for stratified sampling – and even golden ratio shuffled stratified sampling – you have to know the number of samples you want to take in advance and can’t naturally extend it and add more.

Stratifed sampling is randomized within the buckets, so we could repeat the sequence again to get new samples, but we are using the same buckets, and we are putting white noise values in them, so our sequence just sort of gets “white noise gains”, instead of the gains that a progressive, open, low discrepancy sequence gives. Below we repeat golden ratio shuffled stratification twice (purple) and 10 times (brown). You can see that golden ratio shuffled stratification loses quality when you repeat it. You really need to know how many samples you want at max, when doing golden ratio shuffled stratified sampling, but you are free to use less than than number.

By doing a golden ratio shuffle on stratified sampling, we did make it progressive (“good” at any number of samples), but we also made it progressive from any index (“good” starting from any index, for any number of samples). That is a pretty neat property, and comes from the fact that our golden ratio shuffle iterator is actually a rank 1 lattice, just like the actual golden ratio sequence, and this is a property of all rank 1 lattices.

However, by golden ratio shuffling stratification, we also made it TOROIDALLY progressive. What i mean by that is that the sampling sequence is finite, but that you can start at any index and have “good” sampling for any number of samples EVEN WHEN THE SEQUENCE FINISHES AND STARTS OVER. There is no “seam” when this sequence starts over. It just keeps going at the full level of quality. This is due to the fact that our “golden ratio shuffle iterator” rank 1 lattice uses a number that is coprime to N to visit all the indicies [0, N) exactly once before repeating.

This torodial progressiveness is useful if you have a lot of things doing integration at once, all using the same sampling sequence for the function, but individually, they may be (re)starting integration on different time intervals. That may sound strange and exotic, but that is exactly what is happening in temporal anti aliasing (TAA). We have a global sub pixel camera jitter, which is the x we plug into the y=f(x) as we integrate every pixel over its footprint, but each pixel individually uses neighborhood color clamping and other heuristics to decide when it should throw out the integration history and start over.

The only challenge is that if we wanted to use something like this for TAA, we would need a 2D sequence for the camera jitter instead of 1D. I do happen to have a blog post on a 2D version of the low discrepancy shuffler. I don’t think that will magically be the answer needed here, but perhaps you can smell what I’m cooking 😛

A Two Dimensional Low Discrepancy Shuffle Iterator (+Random Access & Inversion): https://blog.demofox.org/2024/10/04/a-two-dimensional-low-discrepancy-shuffle-iterator-random-access-inversion/

I should note there are other ways to do progressive stratified sampling, for instance the great 2018 paper “Progressive Multi-Jittered Sample Sequences” by Per Christensen, Andrew Kensler and Charlie Kilpatrick. https://graphics.pixar.com/library/ProgressiveMultiJitteredSampling/paper.pdf

In the post so far, we’ve only looked at integrating the “triangle” function y=x. Below are the results for that again, and also for a step function, a sine function, and a Gaussian function. Different sampling sequences behave better or worse with different types of integrands sometimes.

Final Error Amounts:

	Gauss	Sine	Step	Triangle
WhiteNoise	0.001232	0.002671	0.002425	0.000843
GoldenRatio	0.000008	0.000024	0.000052	0.000023
Stratified	0.000001	0.000011	0.000033	0.000017
StratifiedGR	0.000001	0.000011	0.000033	0.000017

Thresholding Modern Blue Noise Textures

The noise textures used in this post, and the python scripts used to generate the diagrams, can be found on github at https://github.com/Atrix256/Threshold_STBN_FAST

Thresholding blue noise textures can be a decent way of getting blue noise points at runtime in real-time rendering. They aren’t the highest quality point sets, but they are fast to make and they can use a density map for the threshold value to make non uniform blue noise points, so they are very convenient.

At various times over the past year or so I’ve stumbled on evidence that seemed to show that thresholding FAST noise textures made lower quality blue noise point sets than when thresholding STBN noise textures.

STBN is “Spatiotemporal Blue Noise Masks”, which aims to have N slices of perfectly good blue noise textures, where each pixel individually is also blue over time. We published it in 2022, and it worked well. https://www.ea.com/seed/news/egsr-2022-blue-noise

FAST is “Filter Adapted Spatiotemporal Sampling”, which eclipses STBN by working for arbitrary spatial and temporal filters, while also increasing the quality of noise textures over STBN, particularly of the vector valued noise textures. We published it in 2024 and it was a nice improvement over STBN. https://www.ea.com/seed/news/spatio-temporal-sampling

So, it was a little bit confusing that thresholding FAST noise textures would be lower quality than STBN, when everything else seemed to show that FAST was better or equal to STBN in every single way.

This post is to finally do those threshold tests and share the results. First lets talk about all the noise types involved. Here they are along with their power spectrums (DFT magnitude).

You can click on the images in this post to view them full sized.

Note that all DFTs in this post are divided by the same value to make them be in the 0 to 1 range, so you can compare them to each other.

FAST S – A 128×128 spatial blue noise texture optimized by the FAST optimizer for a Gaussian low pass filter with a sigma of 1.0.
FAST ST – The first slice of a 128x128x32 FAST noise texture like FAST S, but optimized over time for a Gaussian filter with a sigma of 1.0 as well, with the filters “separate 0.5” (added) not “product” (multiplied).
STBN 1.0 S – A 128×128 spatial blue noise texture optimized by the STBN optimizer (a void and cluster variant) with a sigma of 1.0.
STBN 1.0 ST – The first slice of a 128x128x32 STBN texture also optimized for a gaussian filter over time with sigma 1.0.
STBN 1.9 S / ST – the same as STBN 1.0, but using a sigma of 1.9 instead.
VNC 1.0 S / 1.5 / 1.9 – 128×128 spatial blue noise made using the void and cluster algorithm made with sigmas 1.0, 1.5, and 1.9 respectively. The void and cluster paper recommends 1.5 and the “free blue noise textures” site uses 1.9. I’m including 1.0 as another data point.
Tellusim ST – The first slice of a 128x128x64 spatiotemporal blue noise texture, using a custom algorithm, from https://tellusim.com/improved-blue-noise/. This noise is actually 16 bit greyscale instead of 8 bit, which gives it many more unique values than the others. Up to 65,536 instead of 256.
Fidussion ST – The first slice of a 64x64x16 spatiotemporal blue noise texture, using a custom algorithm, from https://acko.net/blog/stable-fiddusion/

Next up, let’s threshold these noise textures. The first row labeled “<= 1” means “if the pixel value is <= 1, write a black dot, else write a white dot”. The second row labeled “2” means “if the pixel value is <= 2, write a black dot, else write a white dot” and so on.

Here are power spectrums of those thresholded values.

Observations

We should start out by noting that thresholding is just one way to measure the quality of blue noise textures. If you are using a noise texture for stochastic transparency by testing alpha against the noise texture to see if you should discard a pixel or not, thresholding quality matters to your result. If you are dithering, the thresholding quality won’t matter for your result

This is important because in the first diagram that shows the power spectrum of the noise textures, the Fidussion texture shows itself to be very high quality blue noise – it has a very dark center circle showing very little low frequency content, and the circle is about as large as it can be within the square. When you use this noise, it pushes as much of the “rendering error” that it can into the highest frequencies, so that it’s more easily removed with a Gaussian low pass filter, and perhaps is higher perceptual quality as well.

However, when we look at the thresholding tests, Fidussion does the most poorly by far. I believe the noise is able to do better as a whole because it doesn’t try to satisfy the thresholding quality constraints. So, if thresholding quality matters to your usage case, you wouldn’t reach for the Fidussion noise, but otherwise, it might look pretty attractive! Basically “Quality is as quality does”.

Overall, none of the textures seem to do very well when extremely sparse, like when <= 1 or <= 254. That is 0.004 and 0.996 in floating point. They all do pretty ok between 10 and 245 though, which is 0.039 and 0.961 in floating point.

VNC 1.9 and Tellusim seem to do pretty ok at the extreme sparse values. VNC 1.9 is not spatiotemporal noise, but Tellusim is. Tellusim doesn’t show as nice DFT in the middle range though. You can see the circle of suppressed low frequencies is not as dark.

In the end, I don’t really see that STBN is better than FAST when thresholded. I think I saw FAST in the extremely sparse zone and didn’t recall ever seeing STBN in the same situation, so it seemed worse.

One other thing these diagrams show though is that if you add temporal constraints to spatial noise, the spatial properties of the noise seem to suffer. I am not certain, but I think that is probably unavoidable – the more constraints you put on something, you eventually reach a saturation point where the constraints can’t be solved, or can’t be solved as well. It would be great if I’m wrong though!

FAST does let you specify how much weight to give the spatial filter versus the temporal filter when doing “separate” mode like this instead of “product”. It defaults to 0.5 which is a balanced weighting between the two. Maybe playing with that could give better results in some situations.

I’d bet there’s a way to make blue noise (spatiotemporal or spatial only) that solved the thresholding constraint better, maybe at the cost of making the overall DFT of the noise texture worse. If you are only ever going to use the noise for thresholding, you don’t need it to have good qualities for other uses.

Links

My void and cluster implementation: https://github.com/Atrix256/VoidAndCluster.git

“Free Blue Noise Textures”: spatial blue noise textures of various kinds, and a python void and cluster implementation: https://momentsingraphics.de/BlueNoise.html

The original void and cluster paper from 1993: https://cv.ulichney.com/papers/1993-void-cluster.pdf

Considering Democrats Blameless is a Medically Useless Diagnosis for the USA

When looking at the politics of the American right and the American left, there is no contest for me as to which to support, if these are my only options.

I see the right doing hateful, authoritarian things that seem to violate their own principles. They violate their religious principles as a largely Christian group who say they want to emulate Jesus but then seem to do the exact opposite at every turn. WWJD seems to be about counterexamples. Non-religious principles are also violated, such as personal liberty, small government, and upholding the constitution (all of it), while trying to force their will on everyone else. Republicans are currently pushing us into a dictatorship, thwarting the balance of powers that were set up by colluding across government branches to dismantle the country, and really seeming to be going against everything our constitution is about, cackling in our face the whole time, right out in the open. Most recently this was about the white house openly declaring they wanted to be able to “deport” (sic) citizens to prisons in other countries (source: https://bsky.app/profile/onestpress.bsky.social/post/3lmd2n77ko22g). I am for personal freedom, liberty, small government, and the values of the Constitution. If Republicans stood for what they claim to, I might very well vote Republican, and do so proudly. These people just have a way of twisting these values to be about serving them only, at the cost of others losing these same things, and more.

I see the left (Democrats) trying to do a little bit of good, although they are largely pro corporation (vs the individual), and also support / do shady things militarily to other countries. It isn’t lost on me that the DMCA was signed into law by Bill Clinton which calls for search and seizure without a warrant, or that the over-response to 9/11 hasn’t been curbed at any of the possible points with democrats in power.

There is a lesser of two evils here that I see, and that is Democrats – and it isn’t even close. They aren’t perfect, but they aren’t actively, overtly, trying to do evil and destroy our country. I don’t see any realistic alternatives either.

However, there is a belief that the Democrats did everything they could do to stop Trump and all of this from happening and that other things are to blame – like perhaps not enough voters turned out, and so it’s the fault of the voters.

No matter what the reason is for the loss, for us to consider the Democrats blameless in the current state of affairs is to accept a useless medical diagnosis for the country. It essentially says that we did everything we could, we still lost, and there is no way to win. Where does that leave us other than giving up? What’s the next step besides smugly watching the world burn and saying “I told you so”? Hopelessness is a terminal diagnosis without a treatment plan.

Consider the CEO of a failing company blaming the customers for not buying the product, or the employees for not performing well enough. Even if these things are true, it’s within the CEO’s responsibility to make the company succeed as well as possible, under any circumstances. Just because a failure can be explained doesn’t excuse the responsibility of failure.

Similarly, the democratic leaders we trusted to help preserve our country have failed. They may have failed despite their best efforts, but they still failed.

Consider this: If the Republican misinformation machine of Fox News et al. can mobilize and motivate people into action, why can’t the Democrats?

I’d like to see a stronger party more about individual empowerment, tougher on corporations and their monetary influence in politics, breaking up actual monopolies, and with the energy and cunning to fight literal evil and a stronger conscience to actually do what is right.

Winning is possible, but the Democratic party opposing the Republicans is not up to the task. So the question becomes: What do we do now? I’m not sure, but I’m not giving up, and I hope you aren’t giving up, either. Let’s keep our eyes open and do what we can, even if only small acts of kindness to foster the world we want, until larger ideas come into view that we can all get behind.

If you have other ideas, speak up. We need a bit of a country wide brainstorming session right now to figure out how to attempt to fix this mess.

Simulating Dice Rolls With Coin Flips

FYI this blog is proudly woke: Trans rights are human rights, Israel needs to stop the genocide in Palestine, Trump is everything the founding fathers of the USA were trying to protect the country against, and black lives matter.

Still here? Cool. Hello and welcome!

Imagine you sit down to board game night, pop open the box, and the dice are missing. Ack, what do you do? Don’t worry, I got you fam. We can simulate dice with coins, or coin like objects.

I want you to consider a problem: How can you simulate rolling a 6-sided dice using 3 coins? Keep that in your head as you read, and see if you can think of a way to do it before I give away the answer lower down on the page.

If you have one coin, you can flip a 2 sided dice. Tails could be 0, and Heads could be 1. (Add 1 to the numbers if you want to get a 1 or a 2).

If you have two coins, you can flip a 4 sided dice. You multiply one of the coins by 2, and add the other to it. If you know binary, these coins are just binary digits.

Coins	Binary Digits	Numbers	Result	Dice #
Tails, Tails	00	0 + 0	0	1
Tails, Heads	01	0 + 1	1	2
Heads, Tails	10	2 + 0	2	3
Heads, Heads	11	2 + 1	3	4

If you have three coins, you can flip an 8 sided dice in the same way.

Coins	Binary Digits	Numbers	Result	Dice #
Tails, Tails, Tails	000	0 + 0 + 0	0	1
Tails, Tails, Heads	001	0 + 0 + 1	1	2
Tails, Heads, Tails	010	0 + 2 + 0	2	3
Tails, Heads, Heads	011	0 + 2 + 1	3	4
Heads, Tails, Tails	100	4 + 0 + 0	4	5
Heads, Tails, Heads	101	4 + 0 + 1	5	6
Heads, Heads, Tails	110	4 + 2 + 0	6	7
Heads, Heads, Heads	111	4 + 2 + 1	7	8

This all works just fine, and each number that might come up has equal probability of coming up (it is a uniform distribution) so it gives fair rolls. But, it only works if you need dice that have a size that are power of 2. What do you do if you want to roll a 6 sided dice?

So, going back to the puzzle at the beginning: How do you simulate rolling a 6 sided dice using 3 coins?

You might think “each coin has 2 options, and there are three of them, so just add them up!”

If tails are 0 and heads are 1, the lowest number you can get is 0, and the highest number you can get is 3. You could add 1, to make it so this was a dice that gave you random numbers between 1 and 4, but it turns out to not have a uniform distribution!

Coins	Numbers	Result	Dice#
TTT	0 + 0 + 0	0	1
TTH	0 + 0 + 1	1	2
THT	0 + 1 + 0	1	2
THH	0 + 1 + 1	2	3
HTT	1 + 0 + 0	1	2
HTH	1 + 0 + 1	2	3
HHT	1 + 1 + 0	2	3
HHH	1 + 1 + 1	3	4

As you can see, there is only 1 way to get a one, and only 1 way to get a four, but there are 3 ways to get a two, and 3 ways to get a three. That means it’s 3 times as likely to get a 2 or 3, than it is to get a 1 or a 4.

So, adding up 3 coins doesn’t give us a 6 sided dice. It gives us a 4 sided dice, that doesn’t even give fair rolls. Lame!

There is a simple answer though: rejection sampling.

You flip 3 coins and that gives you a number between 1 and 8. If the number is 7 or 8, you ignore it and flip the 3 coins again.

Doing this, the numbers you KEEP (1 through 6) come up with equal probability (1/6th). The only downside is you don’t know how many times you might have to flip the coins to get a valid dice roll. That isn’t the worst thing in the world though. Sometimes when rolling dice, it falls off the table and goes under the couch or something and you have to reroll anyways. You can think of it in the same kind of way.

Advanced Tactic: When you throw out the 7 or 8, you aren’t completely empty handed. That 7 or 8 is actually 1 bit of random information you can keep. It’s essentially a uniform random coin flip, and it has no correlation with the 6 sided dice rolls, or any previous or future bit of info generated in this way. You could stash this bit away somewhere if you wanted – like write down the stream of 7s and 8s on a piece of paper, aka 0s and 1s, and then have a random bit stream for cryptographic purposes later, as a treat. Or you can use that as one of the coin flips for the reroll – flip 2 coins instead of three, and use this bit as the third coin.

So that works for a 6 sided dice, but how about a 20 sided dice?

Well, flipping 5 coins is the same as rolling a 32 sided dice and you can still use rejection sampling. If the number is between 1 and 20, keep it. If it’s bigger than 20 ignore it.

Advanced Tactic: Similarly to flipping 3 coins to either get a 6 sided dice roll, or a coin flip, the information we throw away simulating a 20 sided dice doesn’t have to be a complete waste. Interestingly, if you flip 5 coins to simulate a 20 sided dice, you throw out values between 21 and 32. If you subtract 20 from the number you throw away, you get values between 1 and 12. That’s right! Flipping 5 coins to simulate a d20 will give you a d12 when it fails that you can write down and save for later.

Flipping coins to simulate dice can also help you roll dice that would be very difficult to make in real life, such as 3 sided dice (which you can do with 2 coin flips) or 100 sided dice (which you can do with 7 coin flips).

It’s possible that each time you flip the coins, you only get heads for a very long time, and are there flipping coins for literally years, but it’s very improbable. In the context of computer programming, this “unknown and unbounded” run time is not great, but sometimes, it’s the best strategy there is. Like for instance if you can pick a random uniform point in a square, but you need a random uniform point in a star shape that was drawn by an artist, you can use rejection sampling to make it happen. (for non uniform points in arbitrary shapes, check out blue noise point sets!)

You can actually calculate how much (on average) the rejection sampling will fail though. It’s just the percentage of the values that you throw away.

6 Sided Dice: You use three coins to make 8 values, and throw 2 of them away (7 and 8), which means you should only have to reroll 2/8 or 1/4 of the time.
20 Sided Dice: You use 5 coins to make 32 values, and throw away 12 of them. So you reroll 12/32 or 3/8 of the time.
3 Sided Dice: You use 2 coins to make 4 values and throw away 1 of them. So you reroll 1/4 of the time.
100 Sided Dice: You roll 7 coins to make 128 values and you throw away 28 of them. So you reroll 28/128 or 7/32 of the time.

When you keep the randomness generated from your rejections, you don’t lose anything really, but these formulas should help you understand how much random information is being generated in each stream over time, which in a computerized system could cause latency or thread starvation type scenarios.

One final thing – what do you do if you only have unfair coins (or coin like objects) that don’t have equal odds for coming up heads vs tails? Well, we take a hint from John Von Neumann and flip two coins (or one twice). If they mismatch, you use the first coin as the coin flip, else you ignore it and flip twice again. https://en.wikipedia.org/wiki/Fair_coin#Fair_results_from_a_biased_coin

Dice, (De)Convolution and Generating Functions

I stumbled across a very cool YouTube video today that talks about how to look for alternate ways of labeling sides of two dice to give you the same random number distribution as if you added two standard dice together. https://www.youtube.com/watch?v=xVRRykIyll0

Making customized dice give desired probability distributions is an interesting topic (like for game design!), but the math that was used in the video was also pretty neat. I’ll walk you through what they did and then we can talk about why it works, from two different points of view.

(I’m going to refer to a single die as “a dice”, apologies in advance!)

The Problem Statement

If you roll a single dice, the probability of getting each possible value is the same: 16.666…%.

However, if you roll two dice and add them together, the probability of getting each possible value is not equal. You can only get a two by rolling a 1 and a 1, but you can roll a four by rolling a 1 and a 3, a 2 and a 2, or a 3 and a 1. There is only one way to roll a two, but there are three ways to roll a four. So, rolling a four is three times more likely than rolling a two. The probability for each possible value is described by the binomial probability distribution below.

Dice Sum	# Of Ways	Probability (Rounded)	Dice Values
2	1	3%	11
3	2	6%	12, 21
4	3	8%	13, 22, 31
5	4	11%	14, 23, 32, 41
6	5	14%	15, 24, 33, 42, 51
7	6	17%	16, 25, 34, 43, 52, 61
8	5	14%	26, 35, 44, 53, 62
9	4	11%	36, 45, 54, 63
10	3	8%	46, 55, 64
11	2	6%	56, 65
12	1	3%	66

The problem statement is this: Is there a different way to label two dice such that when you add them together, you get the exact same probability distribution as when using standard dice?

It turns out there is exactly one other way to label the dice, and they are called “Sicherman Dice”, named after the person who invented them, in 1978.

Dice A: 1, 2, 2, 3, 3, 4
Dice B: 1, 3, 4, 5, 6, 8

How To Find These Dice

The video explains that you can turn a dice into a polynomial summing up terms of the form $a_k*x^k$ . The value $k$ is what number is on the dice face, and the value $a_k$ says how many faces have that value.

For instance, a standard dice which has faces 1,2,3,4,5,6 would have this polynomial below, which states that it has one of each number 1 through 6:

$x+x^2+x^3+x^4+x^5+x^6$

If we changed the 2 face to be a 4, we’d have the polynomial below, which says we have faces 1,3,4,4,5,6:

$x+x^3+2x^4+x^5+x^6$

These polynomials are valuable because if you have two of them, you can multiply them together to get a “virtual dice” that is the same as if we added the dice together into a single dice.

If we multiply two standard dice together:

$(x+x^2+x^3+x^4+x^5+x^6) * (x+x^2+x^3+x^4+x^5+x^6)$

We get the polynomial:

$x^2 + 2x^3 + 3x^4 + 4x^5 + 5x^6 + 6x^7 + 5x^8 + 4x^9 + 3x^{10} + 2x^{11} + x^{12}$

If you add up how many faces there are, that would be a 36 sided dice, and if you look at the number of faces of each value, you can see they follow the same binomial distribution that we showed in the problem statement section, when adding two dice together.

We aren’t done yet though, we need to see if there’s an alternate way to break this 36 sided dice polynomial back into two 6 sided dice, that aren’t just the standard 6 sided dice.

We need to factor that large polynomial into two smaller ones. These smaller polynomials have requirements (constraints) as well, to be valid:

Each $a_k$ needs to be non negative. That is, you can’t have a negative number of face values on a dice. That’d be weird.
The labels need to be positive. 0 is not a valid face value. This means that $a_0 = 0$ so that $a_0*x^0$ is 0.
The dice should have 6 faces. So if you sum up $a_k$ for all $k$ , it should give you 6.

The second bullet point can be described as $f(0) = 0$ because it makes all the $x$ power terms go away and leaves only the value of $a_0$ .

The third bullet point can be described as $f(1) = 6$ because that will make all $x$ power terms become 1, and so it will just be the $a_k$ values summed up.

The first step is to decompose the large polynomial into irreducible (prime) factors. In the video, instead of factoring the large polynomial, he factors the standard dice polynomial instead, and duplicates the factors, to get the list below. This video is a good intro to factoring polynomials if you need it: https://www.youtube.com/watch?v=KUMhpKGwpCY

$x$
$(1+x)$
$(1-x+x^2)$
$(1+x+x^2)$
$x$
$(1+x)$
$(1-x+x^2)$
$(1+x+x^2)$

To make new dice, we are going to assign each of those factors above to one of the dice. The factors assigned to a dice are going to be multiplied together to get the final polynomial for the dice.

We start with the second constraint that $f(0)=0$ . The only way that can be true is if each dice has the $x$ factor. So, we assign one of those to the first dice, and the other one to the second dice.

Dice A: $x$
Dice B: $x$

Let’s move onto the second constraint that $f(1)=6$ . If we plug 1 in for $x$ , the factor we already have for each dice evaluates to 1,and here are the values we get for each of the factors remaining:

$(1+x) = 2$
$(1-x+x^2) = 1$
$(1+x+x^2) = 3$
$(1+x) = 2$
$(1-x+x^2) = 1$
$(1+x+x^2) = 3$

Since we are multiplying factors together, and we need both of the dice to evaluate to 6, that means we assign $(1+x)$ to each dice to multiply by 2, and also assign $(1+x+x^2)$ to each dice to multiply by 3, so that we are multiplying each dice by 6.

Our dice are identical right now, looking like this:

Dice A: $x*(1+x)*(1+x+x^2)$
Dice B: $x*(1+x)*(1+x+x^2)$

We also have two factors left to assign:

$(1-x+x^2)$
$(1-x+x^2)$

If we gave each dice one of these factors, we’d end up at the standard dice again, so the idea is to give both factors to one of the dice to get this:

Dice A: $x*(1+x)*(1+x+x^2)$
Dice B: $x*(1+x)*(1+x+x^2)*(1-x+x^2)*(1-x+x^2)$

We can multiply these out to get the following polynomials:

Dice A: $x + 2x^2 + 2x^3+ x^4$
Dice B: $x + x^3 + x^4 + x^5 + x^6 + x^8$

Listing out the faces of the dice, we find we’ve made the Sicherman dice! Also, all three constraints are satisfied by both dice.

Dice A: 1, 2, 2, 3, 3, 4
Dice B: 1, 3, 4, 5, 6, 8

Explanation As Convolution

When I saw this, it made sense to me in terms of convolution. There are two concepts here to show what I mean.

The first concept is that if you add together two random values, you are also convolving their probability distributions. For discrete random values, such as dice, you are convolving their Probability Mass Function (PMF) which is a normalized histogram. For continuous random values, you are convolving their Probability Density Function (PDF). See this for more information: https://en.wikipedia.org/wiki/Convolution_of_probability_distributions

The second concept is that when you multiply polynomials together, you are actually doing convolution of their coefficients.

For instance, if you wanted to convolve the sequence 1,1 with the sequence 1,1 that would give you the sequence 1,2,1.

We can set this up with polynomials by giving each term in the sequence a unique power of x:

$f(x) = 1*x^0 + 1*x^1 = 1 + x$
$g(x) = 1*x^0 + 1*x^1 = 1 + x$
$h(x) = f(x)*g(x) = (1+x)(1+x) = (1+2x+x^2)$

You can see that the coefficients of the result are 1,2,1 and gave us the same answer as convolution.

As a more complex example to help show this works, let’s convolve 2,2 with 1,2,3,4. That should give us 2, 6, 10, 14, 8. (Here’s an online discrete convolution calculator: https://www.rapidtables.com/calc/math/convolution-calculator.html)

$f(x) = 2*x^0 + 2*x^1 = 2+2x$
$g(x) = 1*x^0 + 2*x^1 + 3*x^2 + 4*x^3 = 1 + 2x + 3x^2 + 4x^3$
$h(x) = f(x)*g(x) = (2+2x)(1 + 2x + 3x^2 + 4x^3) = 2+6x+10x^2+14x^3+8x^4$

We got our answer in the coefficients again: 2, 6, 10, 14, 8.

So, if we want to get the probability distribution of the sum of two dice, we know we need to convolve their distribution. By making the dice histogram into polynomials, we can multiply the polynomials to do the convolution, and get our resulting histogram. The polynomial then just needs to be factored into two polynomials that satisfy the dice validity constraints.

Viewed from this perspective, this method seems like a “hacky party trick”.

Interestingly though, the part about factoring a polynomial into smaller polynomials can be seen as deconvolution in this point of view. Deconvolution is a powerful thing, and kind of an advanced topic, but to bring it to something tangible, if you have a blurry image, and you know the kernel that blurred the image, deconvolution lets you get the unblurred source image back.

As we saw in this situation though, factoring a polynomial into two other polynomials multiplied together does not always give a unique solution, and it isn’t an easy process to find and enumerate the solutions. This is also true in deconvolution, unsurprisingly! There are multiple methods for doing deconvolution. This polynomial factoring is equivalent to just one of the methods.

Generating Functions Introduction

The other way I wanted to talk about this problem is from the point of view of generating functions, which generalize this creative use of exponents into a powerful mathematical tool. Generating functions allow you to abstract certain types of problems as polynomial multiplication.

A generating function is a polynomial just like the ones we’ve been looking at: a sum of powers of x multiplied by coefficients.

$a_0x^0 + a_1x^1 + a_2x^2 + ... + a_nx^n$

When looking at a specific term $a_kx^k$ , the $a_k$ value says how many ways there are to select the value $k$ .

Example 1 – AABB

We’ll work through 2 examples of making generating functions. I’m taking these directly from the video https://www.youtube.com/watch?v=fL2zQii4B5E.

If we have a single letter A that we can select or not, there is 1 way to select 0 elements, and 1 way to select 1 elements. That gives a generating function $1*x^0 + 1*x^1$ which simplifies to:

$1 + x$ .

If we have the letters AA, there is 1 way to select 0 elements, 1 way to select 1 element (because the As are identical to each other), and there is 1 way to select 2 elements. That gives the generating function:

$1 + x + x^2$

If we also have the letters BB, they have the same generating function:

$1 + x + x^2$

To get the generating function for AABB, we are selecting from AA and from BB and adding them together, so we multiply the generating functions together:

$(1 + x + x^2) * (1 + x + x^2)$

Which equals:

$1+2x+3x^2+2x^3+x^4$

That shows us there is:

1 way to select 0 elements
2 ways to select 1 elements (just A or just B)
3 ways to select 2 elements (AA, BB, AB)
2 ways to select 3 elements (AAB or ABB)
1 way to select 4 elements (AABB)

Example 2 – ABCD

Going back to a single letter choice, we can take the letter or leave it, giving us the generating function:

$1 + x$ .

If we have four letters we can choose from (or not) – ABCD – we multiply that generating function by itself four times: once per letter.

$(1 + x)*(1 + x)*(1 + x)*(1 + x)$

That equals:

$1 + 4x + 6x^2 + 4x^3 + x^4$

This shows us there is:

1 way to select 0 elements
4 ways to select 1 element (A, B, C or D)
6 ways to select 2 elements (AB, AC, AD, BC, BD, CD)
4 ways to select 3 elements (BCD, ACD, ABD, ABC)
1 way to select 4 elements (ABCD)

Fun fact: you may notice this is the 5th row of Pascal’s triangle. This relates to binomial expansion and the binomial theorem. This also relates to Bernouli trials, since we are either taking each letter or leaving it. This series of values is also is what happens if you convolve 1,1 against itself, four times!

Problem 1 – Summing Three Numbers

Let’s work through two simple problems to better understand the application of generating functions before talking about the dice problem. These examples come directly from this video https://www.youtube.com/watch?v=-drdeNMoe8w.

For the first problem, we want to know how many ways are there to sum three numbers to get an answer of 12, when each number is between 0 and 6 inclusively.

We want to know how many ways $A+B+C=12$ can be true, when $A,B,C \in [0,6]$ .

Choosing a number between 0 and 6 is represented by the generating function $(1 + x + x^2 + x^3 + x^4 + x^5 + x^6)$ . If we want to do that three times – once for A, once for B, once for C – and add them together, we multiply that generating function by itself three times, aka we cube it.

$(1 + x + x^2 + x^3 + x^4 + x^5 + x^6)^3$

That gives:

$1 + 3x + 6x^2 + 10x^3 + 15x^4 + 21x^5 + 28x^6 + 33x^7 + 36x^8 + 37x^9 + 36x^{10} + 33x^{11} + 28x^{12} + 21x^{13} + 15x^{14} + 10x^{15} + 6x^{16} + 3x^{17} + x^{18}$

The coefficient for $x^{12}$ is 28, which means there are 28 different ways to add the three numbers between 0 and 6 together, to get 12.

Problem 2 – Picking Jelly Beans

Imagine we have a jar of red, blue and white jellybeans. We want to know how many ways there are to select 20 jelly beans such that:

We have an even number of red jelly beans
We have at least 14 blue jelly beans.
We have less than 5 white jelly beans.

Those three constraints become these three generating functions:

$(1+x^2 + x^4 + ... + x^{20})$
$(x^{14}+x^{15}+ ... + x^{20})$
$(1 + x + x^2 + x^3 + x^4)$

The first and second generating functions could extend beyond $x^{20}$ into infinity, but we know there are 20 jellybeans total, so we can stop at 20.

Multiplying those three together gives us the polynomial below, which shows us that $x^{20}$ has a coefficient of 14. There are 14 different ways to select 20 jellybeans while satisfying the constraints.

Explanation As Generating Functions

Looking at the original dice summing problem from the perspective of generating functions, you can see that we have individual dice that have generating functions describing how many ways there are to roll each number.

With a standard 6 sided dice, the generating function only has one way to roll each number:

$1 + x + x^2 + x^3 + x^4 + x^5 + x^6$

For our modified dice where we replaced the 2 face with a 4, that meant there was no way to get a 2 anymore, but there were two ways to get a 4:

$1 + x + x^3 + 2x^4 + x^5 + x^6$

Multiplying dice polynomials together gave the histogram of how many ways each value could come up if you rolled two dice and added them together.

In the example problems of generating functions in the last section, we only concerned ourselves with a single coefficient, because we wanted to know how many ways a specific value could be selected.

In the dice summing problem though, we are concerned with ALL coefficients. The reason for this is because we are trying to get a specific histogram of possible selected values. A histogram is an array of counts, which is what the coefficients are. So, our dice problem is just a generating function problem which concerns itself with multiple coefficients. That’s still well within the realm of normality for generating functions.

The generating function point of view of this problem helps give a more formal footing to this method, rather than the “hacky party trick” point of view, but I don’t believe it helps you factor the final generating function of the summed dice into the two individual generating functions needed for the alternately labeled dice. It’s just another way of explaining why the polynomial shenanigans work.

Closing

If you’ve done any DSP work, as you learn more about generating functions you may notice they are pretty similar to the z transform (the discrete laplace transform). In generating functions, you can shift the index of the coefficient you need to calculate by multiplying by positive or negative powers of x, just like you can multiply by z to shift a sample in time. I have two write ups on the DSP side of things regarding this if you want to know more:

Here are the videos I found most helpful when learning about generating functions. Some of these were linked above in the article already FYI.

There is a method to get a single coefficient without having to calculate them all, using the Extended Binomial Theorem. That is explained in the second link above.

If you liked this post, you would probably also be interested in this post, which talks about summing discrete number sequences using something called “Umbral Calculus”: https://blog.demofox.org/2022/08/09/calculating-discrete-sums-with-umbral-calculus/

Thanks for reading, and hopefully you found this topic as interesting as I did!

Update: Someone shared some pretty cool posts about generating functions and dice for the board game “Arcs”:

Scaling Points In a Specific Direction

In this post I’ll be showing two different ways to scale points along a specific direction (a vector). There isn’t anything novel here, but it gives an example of the type of math encountered in game development, and how you might approach a solution. The first method involves matrices, and the second involves vector projections.

The points in the red circle below are scaled along the dark green vector, with the magnitude of the bright green vector.

The C++ code that made this diagram can be found at https://github.com/Atrix256/ScalePoints. It implements the vector projection method.

This problem came up for me when implementing a Petzval lens effect (https://bbhphoto.org/2017/04/24/the-petzval-lens/) in a bokeh depth of field (https://blog.demofox.org/2018/07/04/pathtraced-depth-of-field-bokeh/) post processing rendering technique. The setup is that I take point samples in the shape of the camera aperture for bokeh and depth of field, and I needed to stretch this sampled shape in a specific direction and magnitude, based on where the pixel is on the screen.

In the end, I just needed to scale points in a specific direction, by a specific amount. If we can do this operation to 1 point, we can do it to N points, so we’ll focus on doing this to a single point.

Method 1 – Matrices

Using matrices to scale a point along a specific direction involves three steps:

Rotate the point so that the direction we want to scale is aligned with the X axis.
Multiply the x axis value by the scaling amount.
Unrotate the point back to the original orientation.

Our vectors are going to be row vectors. For a deep dive on other matrix and vector conventions and reasons to choose one way or another, read this great post by Jasper St. Pierre: https://blog.mecheye.net/2024/10/the-ultimate-guide-to-matrix-multiplication-and-ordering/

Let’s say we want to scale a point by 4 along the vector [3,1].

First we normalize that vector to [3/sqrt(10), 1/sqrt(10)]. Then we need to get the rotation matrix that will transform [3/sqrt(10), 1/sqrt(10)] to [1,0]. We can do that by making a matrix where the first column is where we want the x axis to point, and the second column to be where we want the y axis to point. For the x axis, we use the normalized vector we already have. For the y axis, we just need a perpendicular vector, which we can get by swapping the x and y components of the vector, and negating one to get [-1/sqrt(10), 3/sqrt(10)]. This operation of swapping x and y and negating one is sometimes called the “2D Cross Product” even though it isn’t really a cross product, and there is no cross product in 2D. That gives us this rotation matrix:

$R = \begin{bmatrix} \frac{3}{\sqrt(10)} & \frac{-1}{\sqrt(10)} \\ \frac{1}{\sqrt(10)} & \frac{3}{\sqrt(10)} \end{bmatrix}$

Next we need to make the scaling matrix, which we get by multiplying the vector [4,1] by the identity matrix:

$S = \begin{bmatrix} 4 & 0 \\ 0 & 1 \end{bmatrix}$

Lastly we need to calculate the unrotation matrix. We need a matrix that rotates by the negative amount of R. We need the inverse matrix of R. The inverse of a rotation matrix is just the transpose matrix, so we can transpose R to make it. Another way to think about it is when we made the matrix before with the first column being the x axis and the second column being the y axis, we are now going to make the first row be the x axis, the second row be the y axis. Rows instead of columns. Whichever explanation makes most sense to you, we end up with this:

$R' = \begin{bmatrix} \frac{3}{\sqrt(10)} & \frac{1}{\sqrt(10)} \\ \frac{-1}{\sqrt(10)} & \frac{3}{\sqrt(10)} \end{bmatrix}$

Now that we have all the transformations, we can calculate R * S * R’ to get a final matrix that does the transformation we want. I’ll do it in 2 steps in case that helps you follow along, to make sure you get the same numbers.

$R*S = \begin{bmatrix} \frac{12}{\sqrt(10)} & \frac{-1}{\sqrt(10)} \\ \frac{4}{\sqrt(10)} & \frac{3}{\sqrt(10)} \end{bmatrix}$

$R*S*R' = \begin{bmatrix} \frac{37}{10} & \frac{9}{10} \\ \frac{9}{10} & \frac{13}{10} \end{bmatrix}$

That is our matrix which scales a point along the vector [3,1], with a magnitude of 4. Let’s put the vector [4,5] through this transformation by multiplying it by the matrix.

$\begin{bmatrix} 4 & 5 \end{bmatrix} \begin{bmatrix} \frac{37}{10} & \frac{9}{10} \\ \frac{9}{10} & \frac{13}{10} \end{bmatrix} = \begin{bmatrix} \frac{193}{10} & \frac{101}{10} \end{bmatrix} = \begin{bmatrix} 19.3 & 10.1 \end{bmatrix}$

For those who are counting instructions, processing a point using this process is 2 multiplies and two adds, to do that 2d vector / matrix product.

Creating the matrix took 16 multiplies and 8 adds (two matrix / matrix multiplies aka eight 2d dot products), but usually, you calculate a matrix like this once and re-use it for many points, which makes the matrix creation basically zero as a percentage of the total amount of calculations done, when amortized across all the points.

Method 2 – Vector Projection

I’m a fan of vector projection techniques. There is a certain intuitiveness in them that is missing from matrix operations, I find.

Using vector projection to scale a point along a specific direction involves these three steps:

Project the point onto the scaling vector and multiply that by the scaling amount.
Project the point onto the perpendicular vector.
Add the scaling vector projection times the scaling vector to the perpendicular vector projection times the perpendicular vector.

We will use the same values from the last section, so we want to scale a point by 4 along the vector [3,1], which we normalize to [3/sqrt(10), 1/sqrt(10)]. We will put the point [4, 5] through this process.

Step 1 is to project our point onto the scaling vector. We do that by doing a dot product between our normalized vector [3/sqrt(10), 1/sqrt(10)], and our point [4, 5]. That gives us the value 17/sqrt(10). We then multiply that by the scaling amount 4 to get 68/sqrt(10).

Step 2 is to project our point onto the perpendicular vector. We can once again use the “2D Cross Product” to get the perpendicular vector. We just flip the x and y component and negate one, to get the vector perpendicular to the scaling vector: [-1/sqrt(10), 3/sqrt(10)]. We can dot product that with our point [4, 5] to get: 11/sqrt(10).

Step 3 is to multiply our projections by the vectors we projected onto, and add the results together. Our scaling vector contribution is 68/sqrt(10) * [3/sqrt(10), 1/sqrt(10)] or [204/10, 68/10]. Our perpendicular vector contribution is 11/sqrt(10)*[-1/sqrt(10), 3/sqrt(10)] or [-11/10, 33/10].

When we add the two values together, we get [193/10, 101/10] or [19.3, 10.1].

That result matches what we got with the matrix operations!

As far as instruction counts, we did two dot products for step 1 and 2 which is 4 multiplies and 2 adds total. Step 3 is 4 multiplies. Step 4 is 2 multiplies and 2 adds. This is a total of 10 multiplies and 4 adds which is a lot more than the matrix version, which was just 2 multiplies and 2 adds.

If you optimized this process to do fewer operations by combining work where you could, you’d eventually end up at the same operations done in the matrix math. Algebra is fun that way.

Higher Dimensions?

Using the matrix method in higher dimensions, making the scaling vector is easy, and making the unrotation matrix is still just taking the transpose of the rotation matrix. It’s more difficult making the rotation matrix though.

In 3D, the scaling direction will be a 3D vector, and you need to come up with two other vectors that are perpendicular to that scaling direction. One way to do this could be to take any vector which is different from the scaling vector, and cross product that with the scaling vector. That will give you a vector perpendicular to both, and you can take that as your second vector. To get the third vector, cross product that vector with the scaling vector. You will then have 3 perpendicular vectors, and an orthonormal basis that you can use to fill out your rotation matrix. The first column is the scaling vector, the second column is the second vector found, and the third column is the third column found.

The cross product only exists in the 3rd and 7th dimension though, so if you are working in a different dimension, or if you don’t want to use the cross product for some reason, another way you can make an orthonormal basis is by using the Gram-Schmidt process. There’s a great video on it here: https://www.youtube.com/watch?v=KOkuTXrv5Gg

For the vector project method, you also need the orthonormal basis vectors to do all the vector projections, before you scale the x axis, and then re-combine the projections, so it boils down to the same issues as the matrix method.

From Readers

Nick Appleton (https://mastodon.gamedev.place/@nickappleton) says:

shameless plug of my last blog post (regarding higher order rotation matrices) https://www.appletonaudio.com/blog/2023/high-dimension-rotation-matrices/

This has methods for generating a high order rotation that moves a point to a particular axis. There is rarely a need need for a Gram Schmidt process and computing the matrix can be made quite cheap 🙂

I think the most efficient way to find a rotation matrix that takes a unit vector A and moves it to another unit vector B (in any dimension) is to find the find the reflection matrix that maps A to C (where C=B with a single component negated – doesn’t matter which one) and then flip the sign of the corresponding row of the matrix to turn it into a rotation.

Finding a reflection matrix that does this requires only a single division in an efficient implementation for any dimension.

Mastodon link: https://mastodon.gamedev.place/@nickappleton/113315462425042217

Andrew Gang (https://vis.social/@pteromys) says:

if your use case doesn’t need accuracy for scaling amounts near zero, method 2 has a variant that saves you from having to find perpendicular vectors: point + (scaling amount – 1) * dot(normalized scaling vector, point) * normalized scaling vector.

Mastodon link: https://vis.social/@pteromys/113317364225437813

A Two Dimensional Low Discrepancy Shuffle Iterator (+Random Access & Inversion)

The C++ code that implements this blog post and generated the images can be found at https://github.com/Atrix256/GoldenRatioShuffle2D.

I previously wrote about how to make a one dimensional low discrepancy shuffle iterator at https://blog.demofox.org/2024/05/19/a-low-discrepancy-shuffle-iterator-random-access-inversion/. That shuffle iterator also supported random access and inversion. That is a lot of words, so breaking it down:

Shuffle Iterator – This means you have an iterator that can walk through the items in a shuffle without actually shuffling the list. It’s seedable too, to have different shuffles.
Low Discrepancy – This means that if you are doing something like numerical integration on the items in the list, you’ll get faster convergence than using a white noise random shuffle.
Random Access – You can ask for any item index in the shuffle and get the result in constant time. If you are shuffling 1,000,000 items and want to know what item will be at the 900,000th place, you don’t have to walk through 900,000 items to find out what’s there. It is just as happy telling you what is at the 900,000th place in the shuffle, as what is at the 0th place.
Inversion – You can also ask the reverse question: At what point in the shuffle does item 1000 come up? It also gives this answer in constant time.

After writing that post, I spent some time trying to find a way to do the same thing in two dimensions. I tried some things with limited success, but didn’t find anything worth sharing.

A couple people suggested I try putting the 1D shuffle iterator output through the Hilbert curve, which is a way of mapping 1d points to 2d points. I finally got around to trying it recently, and yep, it works!

You can also use the Z-order curve (or Morton curve) to do the same thing, and it works, but it doesn’t give as nice results as the Hilbert curve does.

People also probably wonder how Martin Robert’s R2 sequence (from https://extremelearning.com.au/unreasonable-effectiveness-of-quasirandom-sequences/) would work here, since it generalizes the golden ratio to 2d, and the 1d shuffle iterator is based on the golden ratio, but I couldn’t find a way to make it work. For example, multiplying the R2 sequence by the width and height of the 2D grid and casting to integer causes the same 2d location to be chosen multiple times, which also leaves other 2d locations never chosen. That is fine for many applications, but if you want a shuffle, it really needs to visit each item exactly once during the shuffle. Below is how many duplicates that had at various resolutions. Random is also included (white noise, but not a shuffle) to compare to.

Texture Size	Pixel Count	R2 Duplicate Pixels	R2 Duplicate Percent	Random Duplicate Percent
64×64	4,096	847	20.68%	36.89%
128×128	16,384	3,379	20.62%	37.01%
256×256	65,536	16,375	24.99%	36.78%
512×512	262,144	29,203	11.14%	36.80%
1024×1024	1,048,576	392,921	37.47%	36.78%
2048×2048	4,194,304	1,831,114	43.66%	36.78%

So first up, here’s an RMSE (root mean squared error) graph, integrating an image in the repo cabin.png (aka finding the average pixel color). RMSE is averaged over 1000 tests to reduce noise in the plot, where each test used a different random seed for the shuffles. White uses a standard white noise shuffle. Hilbert and ZOrder use a 1D low discrepancy shuffle, then use their respective curves to turn it into a 2D point.

Here is the 512×512 image being integrated:

So that’s great… Hilbert gives best results generally, but Z Order also does well, compared to a white noise shuffle.

Some things worth noting:

Both Hilbert and Z order curves can be reversed – they can map 1d to 2d, and then 2d back to 1d. That means that this 2d shuffle is reversible as well. To figure out at what point in a shuffle a specific 2D point will appear, you first do the inverse curve transformation to get the 1D index of that point, and then ask the low discrepancy shuffle when that 1D index will show up.
As I’ve written it, this is limited to powers of 2. There are ways of making Hilbert curves that are not powers of 2 in size but I’ll leave that to you implement 😛

I did omit something from the previous test though… What if we didn’t put the 1d shuffle through any curve? What if we treated the image as one long line of pixels (like it is, in memory) and used a 1d shuffle on that? Well, it does pretty well!

However, you should see the actual point sets we are talking about before you make a final judgement.

Below are the White noise shuffled points (left), Z order points (middle) left, Hilbert points (middle right) and 1DShuffler points (right) at different numbers of points, to show how they fill in the space. The last image in each uses a point’s order as a greyscale color to show how the values show up over time.

Click on the images to see them full sized.

64×64

128×128

256×256

512×512

1024×1024

So, while the 1DShuffler may give better convergence, especially near the full sample count, the point set is very regularly ordered and would make noticeable rendering artifacts. This is very similar to the usual trade off of low discrepancy sequences converging faster but having aliasing problems, compared to blue noise which converges more slowly but does not suffer from aliasing, and is isotropic.

You might notice a strange thing in Hilbert at 1024×1024 where it seems to fill in “in clumps”. 2048×2048 seems to do the same, but 4096×4096 goes back to not clumping. It’s strange and my best guess as to what is going on is that Hilbert mapping 1d to 2d means that points nearby in 1d are also nearby in 2d, but the reverse does not hold. Points far away in 1d are not necessarily far away in 2d? I’m not certain though.

Bonus Convergence Tests

Here’s a 512×512 white noise image to integrate, and the convergence graph below.

Here is the same with a blue noise texture. This blue noise made with FAST (https://github.com/electronicarts/fastnoise). This is the same pixel values as the white noise texture above, just re-arranged into a blue noise pattern.

So interestingly, integrating the white noise texture made the “good samplers” do less good. Integrating the blue noise texture made the “good samplers” do even less well and be equal to white noise sampling.

What gives?

This isn’t proven, and isn’t anything that I’ve seen talked about in literature, but here’s my intuition of what’s going on:

“Good sampling” relies on small changes in sampling location giving small changes in sampled value. This way, when it samples a domain in a roughly evenly spaced way, it can be confident that it got fairly representative values of the whole image.

This is true of regular images, where moving a pixel to the left or right is going to usually give you the same color.

This may or may not be true in a white noise texture, randomly.

A blue noise texture however, is made to BREAK this assumption. Small changes in location on a blue noise texture will give big changes in value.

Just a weird observation – good sampling tends to be high frequency, while good integrands tend to be low frequency. Good sampling tends to have negative correlation, while good integrands tend to have positive correlation.

Summing Blue Noise Octaves Like Perlin Noise

I haven’t made many blog posts this year, due to working on a project at work that I just got open sourced. The project is called Gigi and it is a rapid prototyping and development platform for real time rendering, and GPU programming. We’ve used it to prototype techniques and collaborate with game teams, we’ve used it in published research (FAST noise), and used it to generate code we’ve shared out into the world.

More info on Gigi is here: https://github.com/electronicarts/gigi/

I also used Gigi to do the experiments and make the code that go with this blog post. Both the Gigi source files and the C++ DX12 code generated from those Gigi files are on github at https://github.com/Atrix256/BNOctaves.

Motivation

Link: https://mastodon.gamedev.place/@lisyarus/113057251773324600

Nikita tagged me in this interesting post with a neat looking screenshot. I thought this was interesting and wanted to look deeper so got the details.

The idea is that you start with a blue noise texture. You then add in another blue noise texture, but 2x bigger and multiplied by 1/2. You then add in another blue noise texture again, but 4x bigger, and multiplied by 1/4. Repeat this as many times as desired. While doing this process you sum up the weights (1 + 1/2 + 1/4 + …) and you divide the result by the weight to normalize it.

Results – Blue Noise

Here is a blue noise texture by itself, made using the FAST command line utility (https://github.com/electronicarts/fastnoise). The upper left is the noise texture. The upper right is the DFT to show frequency content, and the bottom half is a histogram. Here we can see that the texture is uniform blue noise. The histogram shows the uniform distribution, and the DFT shows that the noise is blue, because there is a dark circle in the center, showing that the noise has attenuated low frequencies.

With 2 octaves shown below, there are lower frequencies present, and the histogram gets a hump in the middle. The low frequencies increase because when we double the size of the texture, it lowers the frequency content. The reason the histogram is no longer uniform is because of the central limit theorem. Adding random numbers together makes them follow a binomial distribution, and Gaussian at the limit (more info: https://blog.demofox.org/2019/07/30/dice-distributions-noise-colors/).

With 3 octaves shown below, the effects are even more pronounced.

So yeah, adding octaves of blue noise together does produce blue noise! It makes the distribution more Gaussian though, and reduces the frequency cutoff of the blue noise.

Note: It doesn’t seem to matter much if I use the same blue noise texture for each octave, or different ones. You can control this in the demo using the “DifferentNoisePerOctave” checkbox.

Results – Other Noise Types

After going through the work of making this thing, I wanted to see what happened using different noise types too.

White Noise

Here is 1 octave of white noise, then 3 octaves. White noise starts with randomized but roughly equal levels of noise in each frequency. This process looks to make the low frequencies more pronounced, which makes sense since the octaves get bigger and so are lower frequency.

3×3 Binomial Noise

This noise type is something we found to rival “traditional” (gaussian) blue noise while writing the FAST paper. Some intuition here is that while blue noise has a frequency cutoff equal distance from the center (0hz aka DC), this binomial noise frequency cutoff has roughly equal distance from the edges (aka nyquist). More info on FAST here https://www.ea.com/seed/news/spatio-temporal-sampling.

Below is 1 octave, then 3 octaves. It seems to tell the same story, but the 3 octaves seem to have some concentric rings in the DFT which is interesting.

3×3 Box Noise

Here is noise optimized to be filtered away using a 3×3 box filter. 1 octave, then 3 octaves.

5×5 Box Noise

Here is noise optimized to be filtered away using a 5×5 box filter. 1 octave, then 3 octaves.

Results – Low Discrepancy Noise Types

Here are some types of low discrepancy noise.

Interleaved Gradient Noise

Interleaved gradient noise is a low discrepancy object that doesn’t really have a name in formal literature. I call it a low discrepancy grid, which means we can use it as a per pixel source of random numbers, but it has low discrepancy properties spatially. It was invented by Jorge Jimenez at Activision and you can read more about it at https://blog.demofox.org/2022/01/01/interleaved-gradient-noise-a-different-kind-of-low-discrepancy-sequence/.

Here is 1 octave then 3 octaves. The DFT goes from a starfield to a more dense starfield.

R2 Noise

R2 is a low discrepancy sampling sequence based on the golden ratio (https://extremelearning.com.au/unreasonable-effectiveness-of-quasirandom-sequences/), but you can also turn it into a “low discrepancy grid”. You do so like this:

// R2 Low discrepancy grid
// A generalization of the golden ratio to 2D
// From https://extremelearning.com.au/unreasonable-effectiveness-of-quasirandom-sequences/
float R2LDG(uint2 pos)
{
	static const float g  = 1.32471795724474602596f;
	static const float a1 = 1 / g;
	static const float a2 = 1 / (g * g);
	return frac(float(pos.x) * a1 + float(pos.y) * a2);
}

1 octave, then 3 octaves. The DFT goes from a starfield, to a swirly galaxy. That is pretty cool honestly! The histogram also have a lot less variance than other noise types, which is a cool property.

Wait… Isn’t This Backwards?

When we make Perlin noise, we start with the chunky noise first at full weight, then we add finer detail noise at less weight, like the below with 1 and 8 octaves of perlin noise.

In our noise experiments so far, we’ve been doing it backwards – starting with the smallest detailed noise at full weight, then adding in chunkier noise as lower weight. What if we did it the other way? The demo has a “BlueReverse” noise type that lets you look at this with blue noise. Here is 1, 3 and 5 octaves:

It has an interesting look, but does not result in blue noise!

Use of Gigi – The Editor

I used Gigi to make the demo and do the experiments for this blog post. You can run the demo in the Gigi viewer, or you can run the C++ dx12 code that Gigi generated from the technique I authored.

I want to walk you through how Gigi was used.

Below is the technique in the Gigi editor. The “CS: Display” node makes the noise texture with the desired number of octaves. “Sub: Histogram” makes the histogram graph. “Sub: DFT” makes the DFT. “CS: MakeCombinedOutput” puts the 3 things together into the final images I pasted into this blog post.

If you double click the “Sub: Histogram” subgraph node, it shows you the process for making a histogram for whatever input texture you give it. This is a modular technique that you could grab and use in any of your Gigi projects, like it was used here!

If you double click the “Sub: DFT” subgraph node instead, you would see this, which is also a modular, re-usable technique if ever you want to see the frequency magnitudes of an image. Note: This DFT is not an FFT, it’s a naive calculation so is quite slow.

Use of Gigi – The Viewer

If you click “Open Viewer” in the main technique (BNOctaves.gg) it will open it in the viewer. You can change the settings in the upper left “Variables” tab and see the results instantly. You can also look at the graph at different points in the execution on the right in the “Render Graph” tab, and can inspect the values of pixels etc like you would with a render doc capture. A profiler also shows CPU and GPU time in the lower left. (I told you the DFT was slow, ha!). For each image above in this blog post, i set the parameters like I wanted and then clicked “copy image” to get it to paste into this blog post.

Use of Gigi – The Compiler & Generated Code

I used GigiCompiler.exe to generate “DX12_Application” code for this technique and the results of that are in the “dx12” folder in the repo. You run “MakeSolution.bat” to have cmake create BNOctaves.sln and then can open and run it. Running that, you have the same parameters as you do in the viewer, including a built in profiler.

I did have to make one modification after generating the C++ DX12 code. There are “TODO:”s in the main.cpp to help guide you, but in my case, all I needed to do was copy the “Combined Output” texture to the render target. That is on line 456:

            // TODO: Do post execution work here, such as copying an output texture to g_mainRenderTargetResource[backBufferIdx]
            CopyTextureToTexture(g_pd3dCommandList, m_BNOctaves->m_output.texture_CombinedOutput, m_BNOctaves->m_output.c_texture_CombinedOutput_endingState, g_mainRenderTargetResource[backBufferIdx], D3D12_RESOURCE_STATE_RENDER_TARGET);

Closing

I sincerely believe that “the age of noise” in graphics has just begun. I more mean noise meant for use in sampling or optimized for filtering, but that type of noise may have use in procedural content generation too, like this post explored.

I am also glad that Gigi is finally open sourced, and that I can use this absolute power tool of research in blog posts like this, while also helping other people understand the value it brings. Hopefully you caught a glimpse of that in this post.