Lagrange Interpolation

Lagrange interpolation is a way of crafting a function from a set of data points..

In the past I’ve seen reference to Lagrange interpolation in relation to audio programming like, for helping make a soft knee for a limiter, but it can be used wherever you need to make a function from some data points.

What’s It Do?

Lagrange interpolation is a way of crafting a $y=f(x)$ function from a set of $(x,y)$ data pairs. The resulting function passes through all the data points you give it (like a Catmull-Rom spline does), so can be used to find a function to interpolate between data sets.

You can’t give two value pairs that have the same x value, but the data points don’t have to be evenly spaced.

Also, if you give $N$ data points, you’ll get out a function that is a $N-1$ degree polynomial. So, if you interpolate two data points, you’ll get a degree 1 polynomial (a line). If you interpolate three data points, you’ll get a degree 2 polynomial (a quadratic).

The function will be quite messy, but you can use algebra, or wolframalpha.com (or the like) to simplify it for you to a simpler equation.

Lagrange interpolation is subject to Runge’s Phenomenon, so the more data points you have, the more the interpolation tends to get “squirly” near the edges and shoot off up high or down low, instead of smoothly interpolating between data values.

How’s It Do It?

Well, to make any kind of curve from data points, if we want the curve to pass through those data points, one way would be to come up with a set of functions to multiply each data point by.

Each function must evaluate to 1 when the curve is at that control point, it should be zero when the curve is at any other control point. Between control points, the function can take any value, but if you make it continuous / smooth, the curve will be continuous and smooth, so that’s usually what is desired.

When we have those functions, to get a point on the curve we just multiply each control point by it’s corresponding function (called a basis function), and we sum up the results.

The pseudocode below is how this works and is the basic functionality of most common curve types:

// The basic way to evaluate most any type of curve
float PointOnCurve (float t, float *controlPoints, int numControlPoints)
{
    float value = 0.0f;

    for (int i = 0; i < numControlPoints; ++i)
        value += controlPoints[i] * ControlPointFunction(i, t);

    return value;
}

float ControlPointFunction (int i, float t)
{
  // return the ith control point function evaluated at time t.
  // aka return f(t) for the ith control point.
}

What makes Lagrange interpolation different than other curve types is the basis functions it uses.

The Math

If you aren’t used to seeing a capital pi, or a laplacian style cursive l in equations, it’s about to get a bit mathy!

If you feel like skipping to the next section, I don’t blame you, but if you are feeling brave, you should try and follow along, because I’m going to slowly walk through each and every symbol to help explain what’s going on and why.

Let’s say that you are want to be able to interpolate between $k+1$ data points:

$(x_0, y_0)\ldots(x_k, y_k)$

The formula for calculating a Lagrange interpolated value is this:

$L(x) := \sum_{j=0}^{k} y_j \ell_j(x)$

The capital sigma ( $\sum_{j=0}^{k}$ ) just means that we are going to loop a variable j from 0 to k (including k), and we are going to sum up the total of everything on the right for all values of j. When you see a capital sigma, think sum (note they both start with an s).

The next thing after the sigma is $y_j$ . That is just the y value from our jth control point. That is essentially controlPoints[j].y.

After that comes the last part $\ell_j(x)$ . That is just the function for the jth control point that we multiply the control point by (aka the basis function), evaluated for the specific value x.

Since there is no operator between this function and the control point, that means we multiply them together. So yeah… that crazy math just says “multiply each control point by it’s basis function, and sum up the results”, just like our pseudo code above does!

The second equation we need to look at is the definition of the basis functions for each control point. Here is the formula that describes the jth basis function, for the jth control point:

$\ell_j(x) := \prod_{\begin{smallmatrix}0\le m\le k\\ m\neq j\end{smallmatrix}} \frac{x-x_m}{x_j-x_m}$

First is the capital pi $\prod_{\begin{smallmatrix}0\le m\le k\\ m\neq j\end{smallmatrix}}$ . This means that we are going to do a loop, but instead of adding the results of the loop, we are going to multiply them together. Where a capital sigma means sum, capital pi means product.

The notation for product is a bit different here than in the sigma though which may be a bit tricky to read at first. Instead of explicitly saying that $m$ should go from 0 to $k$ , the notation $latex 0\le m\le k\\$ says that implicitly. That same notation can be used with sigma, or the more explicit style notation could be used with pi.

The pi also has this notation next to it $m\neq j$ . That means that the case where $m$ equals $j$ should be skipped.

Finally, on to the second part: $\frac{x-x_m}{x_j-x_m}$ . This part is pretty easy to read. $x$ is the parameter to the function of course, $x_m$ is just controlPoints[m].x where $m$ is the index variable of our product loop ( $\prod$ ), and $x_j$ is just controlPoints[j].x where $j$ is the index variable of our summation loop ( $\sum$ ).

Let’s say that $k$ was 2 because we had 3 data pairs. Our three basis functions would be:

$\ell_0(x) := \frac{x-x_1}{x_0-x_1} * \frac{x-x_2}{x_0-x_2}$
$\ell_1(x) := \frac{x-x_0}{x_1-x_0} * \frac{x-x_2}{x_1-x_2}$
$\ell_2(x) := \frac{x-x_0}{x_2-x_0} * \frac{x-x_1}{x_2-x_1}$

Which means that our final Lagrange interpolation function would be:

$L(x) := y_0 * \frac{x-x_1}{x_0-x_1} * \frac{x-x_2}{x_0-x_2} + y_1 * \frac{x-x_0}{x_1-x_0} * \frac{x-x_2}{x_1-x_2} + y_2 * \frac{x-x_0}{x_2-x_0} * \frac{x-x_1}{x_2-x_1}$

That is quite a mouth full, but hopefully you understand how we came up with that!

$x_i$ is just controlPoints[i].x and $y_i$ is just controlPoints[i].y.

Math Intuition

The intuition here is that we need to come up with a set of functions to multiply each control point by, such that when the function’s x value is at the control point’s x value, the function should evaluate to 1. When the function’s x value is at a different control points x value, the function should evaluate to 0. The rest of the time, the function can evaluate to whatever it wants, although again, having it have smooth values is nice to making a good curve.

So the first problem is, how do we make a function evaluate to 0 when x is at a different control point?

The easy way would be to multiply a bunch of terms together of this form $(x - x_i)$ , but make sure and not include the x of the actual control point that we are multiplying against.

That is exactly what it does with the numerator in the product notation of the basis function.

$\ell_j(x) := \prod_{\begin{smallmatrix}0\le m\le k\\ m\neq j\end{smallmatrix}} \frac{x-x_m}{x_j-x_m}$

Note that $j$ is the index of the current control point that we are calculating the basis function for. All values of x, that isn’t the x value of a control point will evaluate to non zero.

The denominator value is there so that when x is the value of the control point that we care about, that the function will evaluate to 1.

It does this by figuring out what the value of the numerator will be when x is at the control point, and then makes that be the value that it divides by, so that it’s 1 at that x value.

Not too much to it. Pretty simple stuff, but powerful as well!

Extending to 2D and Beyond

Lagrange interpolation is a one dimensional interpolation scheme, meaning that if you have data points of the form (x,y), it can give you an interpolated y value based on an x value you give it. The interpolation it does can never give two different y values for the same x.

If you want to extend this technique to interpolating a curve through two dimensional data points, or even higher, you need to do interpolation independently for each axis and use a “parametric” value for that axis.

For instance, if you needed to interpolate a curve through 3 dimensional points, you would have data points like this:

X Points = $(t_{x,0}, x_0)\ldots(t_{x,k+1}, x_{k+1})$
Y Points = $(t_{y,0}, y_0)\ldots(t_{y,k+1}, y_{k+1})$
Z Points = $(t_{z,0}, z_0)\ldots(t_{z,k+1}, y_{k+1})$

And then you would interpolate on each axis by the t value to get your X, Y and Z axis values. This should look familiar, because this is how higher dimensional Bezier curves work; you evaluate them per axis based on a parametric value per axis (s,t,u,etc).

You could use the same t values on each axis, or they could be completely independent. You don’t even need to have the same number of points for each axis!

You might wonder how this differs from the standard interpolation in the 2D case. Check the demos in the link section below to really get a grasp of the difference, but in essence, with standard (1D) interpolation, you can never have two x values that evaluate to 2 different y values. Extending it like the above into two dimensions by parameterizing each axis lets you get around that limitation and you can make true 2d shapes.

Lastly, it is possible to make Lagrange interpolated surfaces! I won’t go into the details (perhaps a future post!), but if you know how to make a bezier rectangle by doing a tensor product (basically having X axis Bezier curves, multiplied by Y axis Bezier curves), you can accomplish a Lagrange surface in a really similar way.

Sample Code

This sample code is written for readability, but could easily be optimized for faster execution. Also, from what I hear, the second form of Barycentric Lagrange Interpolation is touted as the fastest form of Lagrange interpolation, since many values can be pre-calculated and re-used for different values of x.

#include <stdio.h>
#include <vector>

struct SPoint
{
    float x;
    float y;
};

typedef std::vector<SPoint> TPointList;

void WaitForEnter ()
{
    printf("Press Enter to quit");
    fflush(stdin);
    getchar();
}

// calculates the lagrange basis function y value for control point "controlPointIndex" at x value "x"
float LagrangeBasis (const TPointList& pointList, size_t controlPointIndex, float x)
{
    // this is the pi "inner loop" multiplication work
    float value = 1.0f;
    for (size_t i = 0, c = pointList.size(); i < c; ++i) {
        if (i != controlPointIndex)
            value *= (x - pointList[i].x) / (pointList[controlPointIndex].x - pointList[i].x);
    }
    return value;
}

// returns a value at x, using lagrange interpolation over the specified list of (x,y) pairs
float LagrangeInterpolate (const TPointList& pointList, float x)
{
    // this is the sigma "outer loop" summation work
    float sum = 0.0f;
    for (size_t controlPointIndex = 0, c = pointList.size(); controlPointIndex < c; ++controlPointIndex)
        sum += pointList[controlPointIndex].y * LagrangeBasis(pointList, controlPointIndex, x);
    return sum;
}

int main (int argc, char **argv)
{
    // show some 1d interpolated values
    // note that the points don't need to be sorted on X, but it makes for easier to read examples
    {
        // (x,y) pairs
        const TPointList points =
        {
            { 0.0f, 1.1f },
            { 1.6f, 8.3f },
            { 2.3f, 6.5f },
            { 3.5f, 4.7f },
            { 4.3f, 3.1f },
            { 5.9f, 7.5f },
            { 6.8f, 0.0f }
        };

        // show values interpolated from x = 0, to x = max x
        printf("1d interpolated values.  y = L(t)n");
        const float c_numPoints = 10;
        for (int i = 0; i < c_numPoints; ++i)
        {
            float percent = ((float)i) / (float(c_numPoints - 1));
            float x = points.back().x * percent;
            float y = LagrangeInterpolate(points, x);
            printf("  (%0.2f, %0.2f)n", x, y);
        }
        printf("n");
    }

    // show some 2d interpolated values
    // also note that x and y don't have to have matching t values!
    {
        // (t, x) pairs
        const TPointList pointsX =
        {
            { 0.0, 0.0f},
            { 1.0, 1.6f},
            { 2.0, 2.3f},
            { 3.0, 3.5f},
            { 4.0, 4.3f},
            { 5.0, 5.9f},
            { 6.0, 6.8f}

        };
        // (t, y) pairs
        const TPointList pointsY =
        {
            { 0.0f, 1.1f },
            { 1.0f, 8.3f },
            { 2.0f, 6.5f },
            { 3.0f, 4.7f },
            { 4.0f, 3.1f },
            { 5.0f, 7.5f },
            { 6.0f, 0.0f }
        };

        // show values interpolated from t = 0, to t = max t, on each axis
        printf("2d interpolated values.  x = L(t_x), y = L(t_y)n");
        const float c_numPoints = 10;
        for (int i = 0; i < c_numPoints; ++i)
        {
            float percent = ((float)i) / (float(c_numPoints - 1));

            // calculate x
            float tx = pointsX.back().x * percent;
            float x = LagrangeInterpolate(pointsX, tx);

            // calculate y
            float ty = pointsY.back().x * percent;
            float y = LagrangeInterpolate(pointsY, ty);

            printf("  (%0.2f, %0.2f)n", x, y);
        }
        printf("n");
    }

    WaitForEnter();
    return 0;
}

And here’s the programs output:

Final Notes

Now that you know how to do all this stuff I wanted to share a couple more pieces of info.

Firstly, it’s kind of weird to call this “Lagrange Interpolation”. A better term is to call this the “Lagrange Form of Polynomial Interpolation”. The reason for that is that if you have some number of data points, there exists only one unique minimal order polynomial (lowest degree of x possible) that fits those points. That is due to the “unisolvence theorem” that you can read more about here: Wikipedia: Polynomial interpolation.

What that means is that if you were to use a different type of polynomial interpolation – such as newton interpolation – the result you get out is algebraically equivalent to the one you’d get from this Lagrange form. There are pros and cons to using different forms of polynomials, but that’s out of the scope of this post so go read about them if you are interested!

Speaking of that, even though this sample code is focused on interpolation using the Lagrange form, this technique is really great at being able to just come up with some simpler f(x) function that passes through specific data points. In this way, you can kind of “bake out” a custom f(x) function to do interpolation for specific values, that doesn’t need all the moving parts of the Lagrange form. For example, if you make the formula for lagrange interpolation of 3 specific value pairs and then simplify, will get out a simple quadratic function in the form of $y=Ax^2+Bx+C$ !

Links

Here are some interactive demos I made to let you play with Lagrange interpolation to get a feel for how it works, and it’s strengths and weaknesses:
One Dimensional Lagrange Interpolation
Two Dimensional Lagrange Interpolation

I also found these links really helpful in finally understanding this topic:
Lagrange Interpolation
Lagrange’s Interpolation Formula

Want to follow the rabbit hole a little deeper? Check out how sinc interpolation relates to the Lagrange form!
The ryg blog: sinc and Polynomial interpolation

The De Casteljau Algorithm for Evaluating Bezier Curves

Over the past year or so I’ve been digging fairly deeply into curves, mostly into Bezier curves specifically.

While digging around, I’ve found many mentions of the De Casteljau algorithm for evaluating Bezier curves, but never much in the way of a formal definition of what the algorithm actually is, or practical examples of it working.

Now that I understand the De Casteljau algorithm, I want to share it with you folks, and help there be more useful google search results for it.

The De Casteljau algorithm is more numerically stable than evaluating Bernstein polynomials, but it is slower. Which method of evaluating Bezier curves is more appropriate is based on your specific usage case, so it’s important to know both.

If you are looking for the mathematical equation of a Bezier curve (the Bernstein form which uses Bernstein basis functions), you have come to the right place, but the wrong page! You can find that information here: Easy Binomial Expansion & Bezier Curve Formulas

Onto the algorithm!

The De Casteljau Algorithm

The De Casteljau algorithm is actually pretty simple. If you know how to do a linear interpolation between two values, you have basically everything you need to be able to do this thing.

In short, the algorithm to evaluate a Bezier curve of any order $N$ is to just linearly interpolate between two curves of degree $N-1$ . Below are some examples to help show some details.

The simplest version of a Bezier curve is a linear curve, which has a degree of 1. It is just a linear interpolation between two points $A$ and $B$ at time $t$ , where $t$ is a value from 0 to 1. When $t$ has a value of 0, you will get point $A$ . When $t$ has a value of 1, you will get point $B$ . For values of t between 0 and 1, you will get points along the line between $A$ and $B$ .

The equation for this is super simple and something you’ve probably seen before: $P(t) = A*(1-t) + B*t$ .

The next simplest version of a Bezier curve is a quadratic curve, which has a degree of 2 and control points $A,B,C$ . A quadratic curve is just a linear interpolation between two curves of degree 1 (aka linear curves). Specifically, you take a linear interpolation between $A,B$ , and a linear interpolation between $B,C$ , and then take a linear interpolation between those two results. That will give you your quadratic curve.

The next version is a cubic curve which has a degree of 3 and control points $A,B,C,D$ . A cubic curve is just a linear interpolation between two quadratic curves. Specifically, the first quadratic curve is defined by control points $A,B,C$ and the second quadratic curve is defined by control points $B,C,D$ .

The next version is a quartic curve, which has a degree of 4 and control points $A,B,C,D,E$ . A quartic curve is just a linear interpolation between two cubic curves. The first cubic curve is defined by control points $A,B,C,D$ and the second cubic curve is defined by control points $B,C,D,E$ .

So yeah, an order $N$ Bezier curve is made by linear interpolating between two Bezier curves of order $N-1$ .

Redundancies

While simple, the De Casteljau has some redundancies in it, which is the reason that it is usually slower to calculate than the Bernstein form. The diagram below shows how a quartic curve with control points $A,B,C,D,E$ is calculated via the De Casteljau algorithm.

Compare that to the Bernstein form (where $s$ is just $(1-t)$ )

$P(t) = A*s^4 + B*4s^3t + C*6s^2t^2 + D*4st^3 + E*t^4$

The Bernstein form removes the redundancies and gives you the values you want with the least amount of moving parts, but it comes at the cost of math operations that can give you less precision in practice, versus the tree of lerps (linear interpolations).

Sample Code

Pretty animations and intuitive explanations are all well and good, but here’s some C++ code to help really drive home how simple this is.

#include <stdio.h>

void WaitForEnter()
{
    printf("Press Enter to quit");
    fflush(stdin);
    getchar();
}

float mix(float a, float b, float t)
{
    // degree 1
    return a * (1.0f - t) + b*t;
}

float BezierQuadratic(float A, float B, float C, float t)
{
    // degree 2
    float AB = mix(A, B, t);
    float BC = mix(B, C, t);
    return mix(AB, BC, t);
}

float BezierCubic(float A, float B, float C, float D, float t)
{
    // degree 3
    float ABC = BezierQuadratic(A, B, C, t);
    float BCD = BezierQuadratic(B, C, D, t);
    return mix(ABC, BCD, t);
}

float BezierQuartic(float A, float B, float C, float D, float E, float t)
{
    // degree 4
    float ABCD = BezierCubic(A, B, C, D, t);
    float BCDE = BezierCubic(B, C, D, E, t);
    return mix(ABCD, BCDE, t);
}

float BezierQuintic(float A, float B, float C, float D, float E, float F, float t)
{
    // degree 5
    float ABCDE = BezierQuartic(A, B, C, D, E, t);
    float BCDEF = BezierQuartic(B, C, D, E, F, t);
    return mix(ABCDE, BCDEF, t);
}

float BezierSextic(float A, float B, float C, float D, float E, float F, float G, float t)
{
    // degree 6
    float ABCDEF = BezierQuintic(A, B, C, D, E, F, t);
    float BCDEFG = BezierQuintic(B, C, D, E, F, G, t);
    return mix(ABCDEF, BCDEFG, t);
}

int main(int argc, char **argv)
{
    struct SPoint
    {
        float x;
        float y;
    };

    SPoint controlPoints[7] =
    {
        { 0.0f, 1.1f },
        { 2.0f, 8.3f },
        { 0.5f, 6.5f },
        { 5.1f, 4.7f },
        { 3.3f, 3.1f },
        { 1.4f, 7.5f },
        { 2.1f, 0.0f },
    };

    //calculate some points on a sextic curve!
    const float c_numPoints = 10;
    for (int i = 0; i < c_numPoints; ++i)
    {
        float t = ((float)i) / (float(c_numPoints - 1));
        SPoint p;
        p.x = BezierSextic(controlPoints[0].x, controlPoints[1].x, controlPoints[2].x, controlPoints[3].x, controlPoints[4].x, controlPoints[5].x, controlPoints[6].x, t);
        p.y = BezierSextic(controlPoints[0].y, controlPoints[1].y, controlPoints[2].y, controlPoints[3].y, controlPoints[4].y, controlPoints[5].y, controlPoints[6].y, t);
        printf("point at time %0.2f = (%0.2f, %0.2f)n", t, p.x, p.y);
    }

    WaitForEnter();
}

Here’s the output of the program:

Thanks to wikipedia for the awesome Bezier animations! Wikipedia: Bézier curve

What is Pre-multiplied Alpha and Why Does it Matter?

The usual equation for blending two pixels with alpha is to use a source factor of “source alpha” and a destination factor of “one minus source alpha”.

That results in this equation:

$\bf{Out.RGB} = In.RGB * In.A + Out.RGB * (1.0 - In.A)$

In other words, it’s just a linear interpolation between $In$ and $Out$ , using the alpha of the pixel you are writing to determine the weighting for the lerp.

Just to be clear, $Out$ is the pixel in your frame buffer (ie the final result that shows up on your monitor) and $In$ is the new pixel you are trying to write or combine with the output image.

If you use pre-multiplied alpha, all that means is that $In.RGB$ is already multipled by $In.A$ which results in slightly less math:

$\bf{Out.RGB} = In.RGB + Out.RGB * (1.0 - In.A)$

Less math for the same results is always a good thing due to increased efficiency, but this also results in a higher quality results in the case of using mips. For more info on that check out this link: NVIDIA GameWorks – Alpha Blending: To Pre or Not To Pre

To achieve this in OpenGL or DirectX with pre-multiplied alpha textures, you just use a source factor of “one” and leave the destination factor at “one minus source alpha”.

If you are using alpha to write to a render target that also has an alpha channel, the math improvement is even better. Here is the equation with regular (post-multiplied) alpha in that scenario for combining the RGB portion of the pixels:

$\bf{Out.RGB} = \frac{In.RGB * In.A + Out.RGB * Out.A * (1.0 - In.A)}{In.A + (1.0 - In.A) * Out.A}$

When working with pre-multiplied alpha it just goes back to the lerp:

$\bf{Out.RGB} = In.RGB + Out.RGB * (1.0 - In.A)$

When blending to a target with alpha, the equation to combine alpha is the old familiar lerp:

$\bf{Out.A} = In.A + Out.A * (1.0 - In.A)$

That makes the lerp form of color combining even nicer since it means the same math for all color channels of the pixel:

$\bf{Out} = In + Out * (1.0 - In.A)$

Confused about why alpha combining using lerp makes sense? It makes most sense to me when thinking about it like this… if you had something that was half opaque(Out.A = 0.5), then you looked at that through something that was 3/4 opaque (In.A = 0.75), only 25% of the light would get past the top layer (0.25), to reach the bottom layer. Only 50% of the light that reached the bottom layer gets through, so we cut that 25% in half to get 12.5% (0.125). Since alpha really means “opaqueness” (1.0 means no transparency), that means that the combined alpha is 1 – 0.125, or 0.875.

If you plug the numbers into the above equation you get the same result:

$\bf{Out.A} = 0.75 + (1.0 - 0.75) * 0.5$
$\bf{Out.A} = 0.75 + 0.25 * 0.5$
$\bf{Out.A} = 0.75 + 0.125$
$\bf{Out.A} = 0.875$

This compute graphics stack exchange question has some more great info on what premultiplied alpha can give you. It’s much more than I wrote here:
Does premultiplied alpha give order independent transparency?

Here’s a fun question… does alpha represent transparency, or does it represent how much of a pixel is covered by an opaque object? To find out the answer give this a read!
Jounral of Computer Graphics Techniques: Interpreting Alpha

A Fifth Way to Calculate Sine Without Trig

In a previous post, I showed Four Ways to Calculate Sine Without Trig. While reading up on rational bezier curves, I came across a 5th way!

A rational bezier curve post will be coming in the (hopefully near) future, so I won’t go into too many details of that, but the important thing to know is that with a rational 2d quadratic bezier curve, you can EXACTLY represent any conic section, including circle arcs. With a regular (integral) bezier curve, you can’t.

You can in fact see that in action in an interactive HTML5 demo i made here: Rational Quadratic Bezier Curve. Note that on my main page, i have links to other 1d/2d bezier/trig rational/integral interactive curve demos. go check them out if you are interested in seeing more: http://demofox.og.

After I made the 2d quadratic bezier demo I realized something… The x and y positions of that curve are calculated independently of each other, and if you wanted to draw a circle in a program, you’d calculate the x and y positions independently, using sine for the y axis value and cosine for the x axis value. That means that if rational curves can – as people say – perfectly represent conic sections, that the two 1d curves that control each axis of that circle arc curve must be exact representations of sine and cosine, at least for the 90 degrees of that arc.

It turns out that this is true enough. I am seeing some variation, but have an open question on math stack exchange to try to get to the bottom of that.

Let’s do some math to come up with our curve based sine equation!

Math Derivation – Skip If You Want To

A rational Bezier equation is defined like this, which is basically just one Bezier curve divided by another:

$\bf{B}(t) = \frac{\sum\limits_{i=0}^n\binom {n} {i}(1-t)^{n-i}t^iW_iP_i}{\sum\limits_{i=0}^n\binom {n} {i}(1-t)^{n-i}t^iW_i}$

So, here is the equation for a rational quadratic bezier curve (n = 2):

$\bf{B}(t) = \frac{(A*W_1*(1-t)^2 + B*W_2*2t(1-t) + C*W_3*t^2)}{(W_1*(1-t)^2 + W_2*2t(1-t) + W_3*t^2)}$

$A,B,C$ are the control points and $W_1,W_2,W_3$ are the weightings associated with those control points.

For the first 90 degrees of sine, $A=0, B=1, C = 1, W_1 = 1, W_2 = cos(arcAngle/2), W_3 = 1$ .

arcAngle is 90 degrees in our case, so $W_2=cos(45)$ or $W_2=1/sqrt(2)$ or $W_2=0.70710678118$ .

If we plug those values in and simplify, and treat it as an explicit (1d) equation of $y = f(x)$ , instead of $P=f(t)$ , we come up with the equation in the next section.

Final Equation

$y = \frac{(0.70710678118*2x(1-x) + x^2)}{((1-x)^2 + 0.70710678118*2x(1-x) + x^2)}$

or, so you can copy paste it:
y=(0.70710678118*2x(1-x) + x^2) / ((1-x)^2 + 0.70710678118*2x(1-x) + x^2)

That gives us the first quadrant (first 90 degrees) of sine. To get the second quadrant, we just horizontally flip the first quadrant. To get the third quadrant, we vertically flip the first quadrant. To get the fourth quadrant, we vertically and horizontally flip the first quadrant.

Equation In Action

Here’s a screenshot from a shadertoy where I implemented this. red = true sine value, green = the value made with the curve, yellow = where they overlap and are equal. Any place you see red or green peaking out means they aren’t quite equal. I sort of expected it to be exactly dead on correct, but like I said, I have an open math stack exchange question to find out why it isn’t and will update this with my findings if they are relevant or interesting. It still is pretty darn good though.

Also, this formula may not be the most efficient way to calculate sine without trig that I’ve shown, but it is interesting, and that’s why I wanted to show it (:

You can see this in action at Shadertoy: Sin Without Trig IV

Easy Binomial Expansion & Bezier Curve Formulas

In this post we are going to explore two things:

Learn how to easily be able to expand $(x+y)^N$ for ANY value $N$ using the binomial theorem (well, N has to be a positive integer…)
Use that for coming up with the equation for a Bezier curve of any degree (any number of control points)

Binomial Theorem

The binomial theorem is a way of easily expanding $(x+y)^N$ . As you probably know, if $N$ is 2, you can use FOIL (first, outer, inner, last). If $N$ gets above 2, things start to get harrier though and more tedious.

Let’s check out how the values look when $N$ is 1, 2 and 3:

$N$	$(x+y)^N$ Expanded
1	$x+y$
2	$x^2+2xy+y^2$
3	$x^3+3x^2y+3xy^2+y^3$

To help make the patterns more visible, let’s make things a bit more explicit:

$N$	$(x+y)^N$ Expanded
1	$1x^1y^0+1x^0y^1$
2	$1x^2y^0+2x^1y^1+1x^0y^2$
3	$1x^3y^0+3x^2y^1+3x^1y^2+1x^0y^3$

The easiest pattern to see is that there are N+1 terms.

The next pattern that might jump out at you looking at the above table, is that in the first term, y starts out at power 0, and the next term has a power of 1, and the power of y keeps increasing by 1 for each term left to right until we run out of terms. Similarly, x starts out at a power of 0 on the last term, has a power of 1 on the second last term, and counts up going from right to left, until we run out of terms.

Those patterns explain how many terms there are and the powers of x and y for each term. There is one piece left of the puzzle though, which is those constants that each term is multiplied by.

Those constants are called the “binomial coefficients” and they also appear as rows on pascal’s triangle. In short, each number in pascal’s triangle is a sum of the numbers directly above it. Below is an image to show what I’m talking about. Check the links section at the end for more detailed info.

So if you notice, the 2nd row of pascal’s triangle is “1,1”. Those are the constants multiplied by each term for the $N=1$ case. The next row down is “1,2,1” which is the constants multiplied by each term for the $N=2$ case. Lastly the next row down (fourth row) is “1,3,3,1” which is the constants multiplied by each term for the $N=3$ case. Essentially, you just use the $N+1$ th tow of pascals triangle to come up with the constants to multiply each term by.

There are algorithms for calculating the $N+1$ th row of the pascal’s triangle. I have one such algorithm in the example code below, but also check the links section for more info on that.

TADA! That is the binomial theorem.

Bezier Curve Equation Generalized (Again)

You may remember that I previously showed you a generalized way to get the equation for a bezier curve of any order in Bezier Curves Part 2 (and Bezier Surfaces).

It wasn’t too difficult, but it DID require you to manually expand $(x+y)^N$ . Now that we know how to do that more easily, thanks to the section above, let’s revise how we come up with bezier curves of any order.

What you do is evaluate $P=(s+t)^N$ , and then multiply each term by a unique control point (A,B,C,etc). After you have your equation, you can optionally replace all $s$ ‘s with $(1-t)$ , or you can just remember that when you evaluate the equation, since the first form is less messy.

Boom, you are done, that’s all!

Here’s the quadratic (N=2) version to see the end result:
$P = As^2 + 2Bst + Ct^2$

Formalized Mathematical Description

The above makes a lot of sense and is easy to understand, wouldn’t it be neat if math could describe it that way?

Well… it turns out it can, and does. Here is the formal “explicit definition” of bezier curves:
$\sum\limits_{i=0}^n\binom {n} {i}(1-t)^{n-i}t^iP_i$

If you remember from above, s is the same as (1-t) so you could also write it like this:
$\sum\limits_{i=0}^n\binom {n} {i}s^{n-i}t^iP_i$

The $\sum\limits_{i=0}^n$ (Sigma, going from 0 to n) means that you are going to sum (add) together n+1 terms (it includes both 0 and n), using i as the loop variable in your summation. It’s basically a for loop, adding together each iteration of the for loop. Everything that comes after is what happens during each iteration of the for loop that gets summed together.

The $\binom {n} {i}$ part means to take the ith number from the (n+1)th row of Pascal’s triangle. More formally, this specifies to use specific binomial coefficients.

The next part $s^{n-i}t^i$ means that you multiply the binomial coefficient by s to the (n-i)th power, and t to the ith power. This is the same as saying s starts at power n and counts down left to right, while t starts at 0 and counts up left to right. This fits the pattern we saw above in binomial expansion.

Lastly comes $P_i$ which means to use the ith P. So, P is basically an array with n+1 elements. This array is the control points, so each P is a different control point.

So, to sum it all up, it’s saying to make a for loop from 0 to n where you are going to add up the results of each for loop. For each loop iteration, where i is the index variation of the loop, you are going to:

Start with the ith item from the (n+1)th row of pascals triangle
Multiply that by s^(n-i)t^i
Multiply that by a unique control point

There ya go, formalized math descriptions with crazy symbols can actually mean something useful. Who would have thought?!

Here is the quadratic bezier curve again for you to look at (quadratic means n = 2), in a form that will help you when thinking about the steps above:
$P = 1s^2t^0A + 2s^1t^1B + 1s^0t^2C$

And when it’s cleaned up, it looks more familiar:
$P = As^2 + 2Bst + Ct^2$

Example Code

#include <stdio.h>
#include <vector>

//=====================================================================================
void WaitForEnter ()
{
    printf("nPress Enter to quit");
    fflush(stdin);
    getchar();
}

//=====================================================================================
std::vector<unsigned int> PascalsTriangleRow(int row)
{
	std::vector<unsigned int> ret;
	ret.push_back(1);
    for (int i = 0; i < row; ++i)
        ret.push_back(ret[i] * (row - i) / (i + 1));
	return ret;
}

//=====================================================================================
void main(void)
{
	printf("Expand (x+y)^N and give Bezier curve order NnnPlease enter N:n");
	unsigned int N;
	// keeping it limited to a sane value. also protects against -1 being huge.
	// Also, so we don't run out of letters for control points!
	if (scanf("%u",&N)==1 && N < 26)
	{
		auto row = PascalsTriangleRow(N);

		// binomial expansion
		printf("nBinomial Expansion:n");
		if (N == 0)
		{
			printf("1");
		}
		else
		{
			for (unsigned int i = 0, c = row.size(); i < c; ++i)
			{
				if (i > 0)
					printf(" + ");

				if (row[i] != 1)
					printf("%u", row[i]);

				unsigned int xPow = N - i;
				if (xPow > 0)
				{
					printf("x");
					if (xPow > 1)
						printf("^%i", xPow);
				}

				unsigned int yPow = i;
				if (yPow > 0)
				{
					printf("y");
					if (yPow > 1)
						printf("^%i", yPow);
				}
			}
		}

		// bezier curves
		printf("nnBezier Curve Order %u:nP = ", N);
		if (N == 0)
		{
			printf("A");
		}
		else
		{
			for (unsigned int i = 0, c = row.size(); i < c; ++i)
			{
				if (i > 0)
					printf(" + ");

				// control point name
				printf("%c*",'A'+i);

				if (row[i] != 1)
					printf("%u", row[i]);

				unsigned int sPow = N - i;
				if (sPow > 0)
				{
					printf("s");
					if (sPow > 1)
						printf("^%i", sPow);
				}

				unsigned int tPow = i;
				if (tPow > 0)
				{
					printf("t");
					if (tPow > 1)
						printf("^%i", tPow);
				}
			}
		}

		// bezier curves
		printf("nnOr:nP = ", N);
		if (N == 0)
		{
			printf("A");
		}
		else
		{
			for (unsigned int i = 0, c = row.size(); i < c; ++i)
			{
				if (i > 0)
					printf(" + ");

				// control point name
				printf("%c*",'A'+i);

				if (row[i] != 1)
					printf("%u", row[i]);

				unsigned int sPow = N - i;
				if (sPow > 0)
				{
					printf("(1-t)");
					if (sPow > 1)
						printf("^%i", sPow);
				}

				unsigned int tPow = i;
				if (tPow > 0)
				{
					printf("t");
					if (tPow > 1)
						printf("^%i", tPow);
				}
			}
		}

		printf("n");
	}
	else
	{
		printf("Invalid value for Nn");
	}
	WaitForEnter();
}

Example Output

Here are some runs of the program

Links

Note that even though we talked about binomials, and bezier curves, these techniques can be expanded to trinomials and bezier triangles – and beyond! (hint: there is such thing as Pascal’s pyramid!)

Here are some links to more info about some of the topics talked about above:
Wikipedia: Binomial Theorem
Wikipedia: Pascal’s Triangle
Wikipedia: Binomial Coefficient
StackOverflow: How to efficiently calculate a row in pascal’s triangle?

Bilinear Filtering & Bilinear Interpolation

Take a look at the picture below. Can you calculate the values at points A,B and C?

There’s a technique for doing this called bilinear interpolation which extends the idea of linear interpolation into two dimensions.

To calculate bilinear interpolation, you just do linear interpolation on one axis, and then the other.

Check out these examples:

Point A
Point A has a coordinate of (0.2,0.8). Let’s start with the X axis.

Firstly, we’ll do interpolation across the top of the square on the X axis. That means we need to go 0.2 (20%) of the way from 7 to 0. That 0.2 is our x axis coordinate. To calculate that we do this:
7 + (0-7) * 0.2 = 5.6

Next, we’ll do interpolation across the bottom of the square on the X axis. So similar to above, we’ll go 0.2 (20%) of the way from 3 to 5. To calculate that we do this:
3 + (5-3) * 0.2 = 3.4

Now that we have interpolated across our X axis we need to interpolate across our Y axis. We are now going to go 0.8 (80%) of the way from our bottom value (the value of Y = 0), to our top value (the value of Y = 1). The bottom value is the bottom interpolation we did (3.4) and the top value is the top interpolation we did (5.6).

So, we need to go 0.8 (80%) of the way from 3.4 to 5.6. To calculate that we do this:
3.4 + (5.6 – 3.4) * 0.8 = 5.16

So, the value at point A is 5.16. The image below should help explain visually the process we went through.

Point B

Point B has a coordinates of (1.0,0.5).

Let’s start with the X axis interpolation again (although you could easily start with Y first if you wanted to! You’d end up with the same result).

Doing the X axis interpolation across the top, we need to go 1.0 (100%) of the way from 7 to 0. I’m sure you can guess what the answer is but here it is calculated:
7 + (0-7) * 1.0 = 0

Similarly, let’s do the X axis interpolation across the bottom. We need to go 1.0 (100%) of the way from 3 to 5.
3 + (5-3) * 1.0 = 5

Next up comes the Y axis interpolation. We need to go 0.5 (50%) of the way from 5 to 0.
5 + (0-5) * 0.5 = 2.5

There we go, the value at point B is 2.5. That should make sense too by looking at the diagram. It’s basically 1d linear interpolation between 5 and 0, and is half way between them, so intuitively, the answer 2.5 should make sense.

Point C

Point C has a coordinate of (0.8,0.2).

Once again, let’s do the X axis interpolation across the top of the box. We need to go 0.8 (80%) of the way from 7 to 0.
7 + (0-7) * 0.8 = 1.4

Then, we need to do the x axis interpolation across the bottom of the box. We need to go 0.8 (80%) of the way from 3 to 5.
3 + (5-3) * 0.8 = 4.6

Lastly, the y axis interpolation. We need to go 0.2 (20%) from 4.6 to 1.4.
4.6 + (1.4-4.6) * 0.2 = 3.96

The value of point C is 3.96

Bilinear Filtering

While bilinear interpolation is useful if you have a grid of data that you want to interpolate values within (such as a height field that represents terrain?!), where this really shines in game development is in bilinear texture filtering.

Basically, when you have a texture coordinate that doesn’t perfectly line up with the center of a pixel in the texture (because there’s a remainder), it uses the fractional part of the coordinate within that pixel to do bilinear interpolation between the 4 pixels involved to come up with the final pixel color. It does bilinear interpolation on each of the channels: Red, Green, Blue and Alpha.

The end result is pretty good! Check out the image below to see it in action on a texture that we are zoomed in too far on. The left side uses bilinear filtering, while the right side does not, and just shows you the nearest pixel.

Consequently, bilinear texture filtering has to do 4 pixel reads to be able to interpolate between them, instead of a single pixel read like when doing nearest pixel sampling. More pixel reads = more overhead, and not as cheap (computationally) to use.

Links

For some folks who are reading this, this info is pretty basic and you might be wondering why i bothered writing about it. Look to the next post for something kind of bizarre regarding bilinear filtering. This was needed as a stepping stone to the next thing I want to show you guys 😛

Wikipedia: Linear Interpolation

Wikipedia: Bilinear Interpolation

Wikipedia: Bilinear Filtering

The Dark Side of Bilinear Filtering

Check out these links for some deeper info about some shortcomings (and some workarounds) of hardware based bilinear sampling:
iq: hardware interpolation
iq: improved texture interpolation

Frequency Domain Audio Synthesis – With IFFT and Oscillators

One way to look at sounds is to think about what frequencies they contain, at which strengths (amplitudes), and how those amplitudes change over time.

For instance, if you remember the details of the post about how to synthesis a drum sound (DIY Synth: Basic Drum), a drum has low frequencies, but also, the frequencies involved get lower over the duration, which gives it that distinctive sound.

Being able to analyze the frequency components of a sound you want to mimic, and then being able to generate audio samples based on a description of frequency components over time is a powerful tool in audio synthesis.

This post will talk about exactly that, using both oscillators as well as the inverse fast Fourier transform (IFFT).

We’ve already gone over the basics of using oscillators to create sounds in a previous post so we’ll start with IFFT. For a refresher on those basics of additive synthesis check out this link: DIY Synth 3: Sampling, Mixing, and Band Limited Wave Forms

All sample sound files were generated with the sample code at the end of this post. The sample code is a single, standalone c++ file which only includes standard headers and doesn’t rely on any libraries. You should be able to compile it and start using the techniques from this post right away!

What is the IFFT?

Audio samples are considered samples in the “time domain”. If you instead describe sound based on what frequencies they contain, what amplitudes they are at, and what phase (angle offset) the sinusoid wave starts at, what you have is samples in the “frequency domain”.

The process for converting time domain to frequency domain is called the “Fourier Transform”. If you want to go the opposite way, and convert frequency domain into time domain, you use the “Inverse Fourier Transform”.

These transforms come in two flavors: continuous and discrete.

The continuous Fourier transform and continuous inverse Fourier transform work with continuous functions. That is, they will transform a function from time domain to frequency domain, or from frequency domain to time domain.

The discrete version of the fourier transform – often refered to as DFT, short for “discrete fourier transform” – and inverse fourier transform work with data samples instead of functions.

Naively computing the DFT or IDFT is a very processor intensive operation. Luckily for us, there is an algorithm called “Fast Fourier Transform” or FFT that can do it a lot faster, if you are ok with the constraints of the data it gives you. It also has an inverse, IFFT.

IFFT is what we are going to be focusing on in this post, to convert frequency domain samples into time domain samples. Also, like i said above, we are also going to be using oscillators to achieve the same result!

Using the IFFT

Here’s something interesting… where time domain samples are made up of “real numbers” (like 0.5 or -0.9 or even 1.5 etc), frequency domain samples are made up of complex numbers, which are made up of a real number and an imaginary number. An example of a complex number is “3.1 + 2i” where i is the square root of negative 1.

If you look at the complex number as a 2d vector, the magnitude of the vector is the amplitude of the frequency, and the angle of the vector is the phase (angle) that the sinusoid (cosine wave) starts at for that frequency component.

You can use these formulas to create the complex number values:

real = amplitude * cos(phase);
imaginary = amplitude * sin(phase);

Or you could use std::polar if you want to (:

BTW thinking of complex numbers as 2d vectors might be a little weird but there’s precedent. Check this out: Using Imaginary Numbers To Rotate 2D Vectors

When using the IFFT, the number of frequency domain samples you decide to use is what decides the frequencies of those samples. After preforming the IFFT, you will also have the same number of time domain samples as frequency domain samples you started with. That might sound like it’s going to be complex, but don’t worry, it’s actually pretty simple!

Let’s say that you have 4 buckets of frequency domain data, that means you will end up with 4 time domain audio samples after running IFFT. Here are the frequencies that each frequency domain sample equates to:

index 0: 0hz. This is the data for the 0hz frequency, or DC… yes, as in DC current! DC represents a constant added to all samples in the time domain. If you put a value in only this bucket and run the IFFT, all samples will be the same constant value.
index 1: 1hz. If you put a value in only this bucket and run the IFFT, you’ll end up with one full cosine wave (0-360 degrees aka 0-2pi radians), across the 4 time domain samples. 4 samples isn’t very many samples for a cosine wave though so it will look pretty blocky, but those 4 samples will be correct!
index 2: 2hz. If you put a value in only this bucket and run the IFFT, you’ll end up with two full cosine waves (0-720 degrees aka 0-4pi radians) across the 4 time domain samples.
index 3: -1hz.

You might wonder what that negative frequency at index 3 is all about. A negative frequency probably seems weird, but it’s really the same as it’s positive frequency, just with a negative phase. It’s basically a cosine wave that decreases in angle as it goes, instead of increasing.

Why is it there though? Well, there’s something called the Nyquist–Shannon Sampling Theorem which states that if you have N time domain audio samples, the maximum frequency you can store in those audio samples is N/2 cycles. That frequency is called the Nyquist frequency and any frequency above that results in “aliasing”. If you’ve ever seen a car tire spin in reverse on tv when the care was moving forward, that is an example of the same aliasing I’m talking about. In manifests in audio as high pitches and in general terrible sounding sound. Before I knew how to avoid aliasing in audio, my now wife used to complain that my sounds hurt her ears. Once i removed the aliasing, she says it no longer hurts her ears. Go back and check the early DIY synth posts for audible examples of aliasing (;

Since we have 4 frequency domain samples, which translates to 4 time domain audio samples, we can only store up to 2hz, and anything above that will alias and seem to go backwards. That’s why index 3 is -1hz instead of 3hz.

So basically, if you have N frequency domain samples (or bins as they are sometimes called), the first bin, at index 0, is always 0hz / DC. Then from 1 up to N/2, the frequency of the bin is equal to it’s index. Then, at N/2+1 up to N-1, there are negative frequencies (frequencies beyond the Nyquist frequency) reflected in that upper half of the bins, starting at N/2 and counting back up to -1.

In many common situations (including the ones we are facing in this post), you don’t need to worry about the negative frequency bins. You can leave them as zero if doing IFFT work, or ignore their values if doing FFT then IFFT work.

Ready for one last piece of complexity? I hope so… it’s the last before moving onto the next step! 😛

Sounds are obviously much longer than 4 samples, so a 4 bin (sample) IFFT just isn’t going to cut it. 1000 bins would to be too few, and Frankly, at 44,100 samples per second (a common audio sampling rate), 88,200 bins is only 2 seconds of audio which isn’t very much at all! Even with the “Fast Fourier Transform” (FFT), that is a huge number of bins and would take a long time to calculate.

One way to deal with this would be to have fewer bins than audio samples that you want to end up with, use IFFT to generate the audio samples, and then use interpolation to get the audio samples between the ones generated by IFFT. We aren’t going to be doing that today but if you like the option, you can most certainly use it!

One of the ways we are going to deal with using a small number of bins to generate a lot of noise is that we are going to use the IFFT to generate wave forms, and then we are going to repeat those wave forms several times.

Another one of the things we are going to do is use IFFT bins to generate a small number of samples, and then modify the IFFT bins to generate the next number of samples, repeating until we have all of our audio samples generated.

In both cases, the frequency buckets need some conversion from the IFFT bin frequencies to the frequencies as they will actually appear in the final audio samples.

To calculate the true frequency of an FFT bin, you can use this formula:

frequency = binNumber * sampleRate / numBins;

Where binNumber is the IFFT bin number, sampleRate is how many samples the resulting sound has per second, and numBins is the total number of IFFT bins.

Simple Wave Forms

The simplest of the wave forms you can create is a cosine wave. You just put the complex number “1 + 0i” into one of the IFFT bins, that represents an amplitude of 1.0 and a starting phase of 0 degrees. After you do that and run ifft, you’ll get a nice looking cosine wave:

Note that the wave repeats multiple times. This is because I repeat the IFFT data over and over. If I didn’t repeat the IFFT data, the number of cycles that would appear would depend completely on which IFFT bin I used. If I used bin 1, it would have only one cycle. If i used bin 2, it would have two cycles.

Also note that since the IFFT deals with INTEGER frequencies only, that means that the wave forms begin and end at the same phase (angle) and thus the same amplitude, which means that if you repeat them end to end, there will be no discontinuities or popping. Pretty cool huh?

If you instead put in the complex number “0 – 1i” into one of the IFFT bins, that represents an amplitude of 1.0 and a starting phase of 270 degrees (or -90 degrees), which results in a sine wave:

We don’t have to stop there though. Once again thinking back to the info in DIY Synth 3: Sampling, Mixing, and Band Limited Wave Forms, the frequency components of a saw wave are described as:

If you have a saw wave of frequency 100, that means it contains a sine wave of frequency 100 (1 * fundamental frequency), another of frequency 200 (2 * fundamental frequency), another of 300 (3 * fundamental frequency) and so on into infinity.

The amplitude (volume) of each sine wave (harmonic) is 1 over the harmonic number. So in our example, the sine wave at frequency 100 has an amplitude of 1 (1/1). The sine wave at frequency 200 has an amplitude of 0.5 (1/2), the sine wave at frequency 300 has an amplitude of 0.333 (1/3) and so on into infinity.

After that you’ll need to multiply your sample by 2 / PI to get back to a normalized amplitude.

We can describe the same thing in IFFT frequency bins believe it or not!

Let’s say that we have 50 bins and that we want a 5hz saw wave. The first harmonic is 5hz and should be full amplitude, so we put an entry in bin 5 for amplitude 1.0 * 2/pi and phase -90 degrees (to make a sine wave instead of a cosine wave).

The next harmonic should be double the frequency, and 1/2 the amplitude, so in bin 10 (double the frequency of bin 5), we put an entry for amplitude 0.5 * 2/pi, phase -90 degrees. Next should be triple the original frequency at 1/3 the amplitude, so at bin 15 we put amplitude 0.33 * 2/pi, phase -90 degrees. Then, bin 20 gets amplitude 0.25 * 2/pi, -90 degrees phase. Bin 25 is the Nyquist frequency so we should stop here, and leave the actual Nyquist frequency empty.

If you run the IFFT on that, you’ll get a bandlimited saw wave!

You can do the same for bandlimited triangle and square waves, and also you can use a random phase and amplitude for each bin to generate noise! The source code for this post generates those in fact (:

Phase Adjusted Wave Forms

While we are dealing in frequency space, I want to run something kind of gnarly by you. Using the technique described above, you can add frequencies with specific amplitudes to make a band limited saw wave. But, believe it or not, the starting phase of the frequencies don’t have to be -90 degrees. If you use a different phase, you’ll get a resulting wave form that looks different but sounds the same. Check these out, it’s a trip!

Here are the sound files pictured above, so you can hear that they really do all sound the same!
270 degrees
0 degrees
60 degrees
120 degrees
180 degrees

Bins Changing Over Time

If you are like me, when you think about designing sound in the frequency domain you think everything must be rainbows and glitter, and that you have no limitations and everything is wonderful.

Well, as happens so many times when the rubber hits the road, that isn’t quite true. Let’s go through an example of using IFFT on some bins that change over time so I can show you a really big limitation with IFFT.

In our example, let’s say that we have a single frequency in our IFFT data (so we are generating a single sinusoid wave) but that we want it’s amplitude (volume) to change over time. Let’s say we want the amplitude of the wave to be controlled by another sinusoid, so that it smoothly goes up and down in amplitude over time.

We immediately hit two problems, but the first is more obvious if you listen:

IFFTTest1.wav

Hear all that popping? It’s basically making a discontinuity at every IFFT window because we are changing the amplitude at the edge of each window. We can’t change it during the window (caveat: without some pretty advanced math i won’t go into), so changing at the end of the window is our only option. Check out this image to see the problem visually:

We can fix those discontinuities. If we change the phase of the wave from cosine (0 degrees) to sine (270 degrees), we make it so that the edge of the window is always at amplitude 0 (sine(0) = 0, while cos(0) = 1!). This means that when we change the amplitude of the wave, since it happens when the wave is at zero, there is no discontinuity, and so no more pops:

Let’s have a listen:
IFFTTest2.wav

WHAT?! There is still some periodic noise… it is tamed a little bit but not fixed. The reason for this is that even though we are first order continuous we aren’t 2nd order continuous (etc). So, by having a jump in amplitude, even constraining it at zero crossings, we’ve essentially added some frequencies into our resulting sound wave that we didn’t want to add, which we can hear in the results.

So yeah… basically, if you want to change your IFFT bins over time, you are going to have some audio artifacts from doing that. Boo hoo!

There are ways around this. One way involves complex math to add frequencies to your bins that make it APPEAR as if you are adjusting the amplitude of the wave smoothly over the duration of the window. Another way involves doing things like overlapping the output of your IFFT windows and blending between them. There are other ways too, including some IDFT algorithms which do allow you to alter the amplitude over time in a window, but are costlier to compute.

Anyways, you can also just generate the sound descibed in your IFFT bins with oscillators, literally adding together all the frequencies with the specified phase offsets to make the correct resulting time domain samples. I’ve done just that to solve the popping problem as well as the issue where you can’t have smooth volume adjustments because you can only change amplitude at the end of each window:

IFFTTest3.wav

You can also see it in action:

Here’s another failure case to check out:

drums_ifft.wav – made with ifft
drums_osc.wav – made with oscillators

Convolution

If you read the post about convolution reverb (DIY Synth: Convolution Reverb & 1D Discrete Convolution of Audio Samples), you’ll recall that convolution is super slow, but that convolution in the time domain is equivelant to multiplication in the frequency domain.

We are in the frequency domain, so how about we try some convolution?!

Let’s multiply the bins of a 1hz saw wave and a 1hz square wave and see what we get if we IFFT the result:

That result is definitely not right. First of all, the convolution is the same length as the inputs, when it should be length(a)+length(b)-1 samples. Basically it should be twice as long as it is.

Secondly, that is not what the convolution looks like. Doing convolution in the time domain of those samples looks like this:

So what’s the deal? Well as it turns out, when you do multiplication in the frequency domain, you are really doing CIRCULAR convolution, which is a bit different than the convolution i described before which is LINEAR convolution. Circular convolution is essentially used for cyclical data (or functions) and basically makes it so that if you try to read “out of bounds”, it will wrap around and use an in bounds value instead. It’s kind of like “texture wrap” if you are a graphics person.

Normally how this is gotten around, when doing convolution in the frequency domain, is to put a bunch of zeros on the end of your time domain samples before you bring them into the frequency domain. You pad them with those zeros to be the correct size (length(a)+length(b)-1, or longer is fine too) and then when you end up doing the “circular convolution”, there are no “out of bounds” values looked at, and you end up with the linear convolution output, even though you technically did circular convolution.

Unfortunately, since we are STARTING in frequency domain and have no time domain samples to bad before going into frequency domain, we are basically out of luck. I’ve tried asking DSP experts and nobody I talked to knows of a way to start in frequency domain and zero pad the time domain so that you could do a linear convolution – at least nobody knows of GENERAL case solution.

Those same experts though say that circular convolution isn’t a bad thing, and is many times exactly what you want to do, or is a fine stand in for linear convolution. I’m sure we’ll explore that in a future post (:

In the example code, i also have the code generate the circular convolution in the time domain so that you can confirm that circular convolution is really what is going on in the above image, when working in frequency domain.

Strike Two IFFT!

Luckily using IDFT to generate sounds (sometimes called Fourier Synthesis) isn’t across the board a losing strategy. If you want a static, repeating wave form, it can be really nice. Or, for dynamic waave forms, if you change your amplitude only a very small amount across window samples, it won’t noticeably degrade the quality of your audio.

The neat thing about IFFT is that it’s a “constant time process”. When using oscillators, the more frequencies you want to appear, the more computationally expensive it gets. With IFFT, it doesn’t matter if all the bins are full or empty or somewhere inbetween, it has the same computational complexity.

Here’s a non trivial sound generated both with IFFT and Oscillators. The difference is pretty negligible right?

alien_ifft.wav – made with IFFT
alien_osci.wav – made with oscillators

Sample Code

#define _CRT_SECURE_NO_WARNINGS
  
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
  
#define _USE_MATH_DEFINES
#include 
  
//=====================================================================================
// SNumeric - uses phantom types to enforce type safety
//=====================================================================================
template 
struct SNumeric
{
public:
    explicit SNumeric(const T &value) : m_value(value) { }
    SNumeric() : m_value() { }
    inline T& Value() { return m_value; }
    inline const T& Value() const { return m_value; }
  
    typedef SNumeric TType;
    typedef T TInnerType;
  
    // Math Operations
    TType operator+ (const TType &b) const
    {
        return TType(this->Value() + b.Value());
    }
  
    TType operator- (const TType &b) const
    {
        return TType(this->Value() - b.Value());
    }
  
    TType operator* (const TType &b) const
    {
        return TType(this->Value() * b.Value());
    }
  
    TType operator/ (const TType &b) const
    {
        return TType(this->Value() / b.Value());
    }

    TType operator% (const TType &b) const
    {
        return TType(this->Value() % b.Value());
    }
  
    TType& operator+= (const TType &b)
    {
        Value() += b.Value();
        return *this;
    }
  
    TType& operator-= (const TType &b)
    {
        Value() -= b.Value();
        return *this;
    }
  
    TType& operator*= (const TType &b)
    {
        Value() *= b.Value();
        return *this;
    }
  
    TType& operator/= (const TType &b)
    {
        Value() /= b.Value();
        return *this;
    }
  
    TType& operator++ ()
    {
        Value()++;
        return *this;
    }
  
    TType& operator-- ()
    {
        Value()--;
        return *this;
    }
  
    // Extended Math Operations
    template 
    T Divide(const TType &b)
    {
        return ((T)this->Value()) / ((T)b.Value());
    }
  
    // Logic Operations
    bool operatorValue() < b.Value();
    }
    bool operatorValue()  (const TType &b) const {
        return this->Value() > b.Value();
    }
    bool operator>= (const TType &b) const {
        return this->Value() >= b.Value();
    }
    bool operator== (const TType &b) const {
        return this->Value() == b.Value();
    }
    bool operator!= (const TType &b) const {
        return this->Value() != b.Value();
    }
  
private:
    T m_value;
};
  
//=====================================================================================
// Typedefs
//=====================================================================================
  
typedef uint8_t uint8;
typedef uint16_t uint16;
typedef uint32_t uint32;
typedef int16_t int16;
typedef int32_t int32;
  
// type safe types!
typedef SNumeric        TFrequency;
typedef SNumeric           TFFTBin;
typedef SNumeric          TTimeMs;
typedef SNumeric            TTimeS;
typedef SNumeric         TSamples;
typedef SNumeric     TFractionalSamples;
typedef SNumeric         TDecibels;
typedef SNumeric        TAmplitude;
typedef SNumeric          TRadians;
typedef SNumeric          TDegrees;
  
//=====================================================================================
// Constants
//=====================================================================================

static const float c_pi = (float)M_PI;
static const float c_twoPi = c_pi * 2.0f;

//=====================================================================================
// Structs
//=====================================================================================
  
struct SSoundSettings
{
    TSamples        m_sampleRate;
    TSamples        m_sampleCount;
};
  
//=====================================================================================
// Conversion Functions
//=====================================================================================

inline TFFTBin FrequencyToFFTBin(TFrequency frequency, TFFTBin numBins, TSamples sampleRate)
{
    // bin = frequency * numBin / sampleRate
    return TFFTBin((uint32)(frequency.Value() * (float)numBins.Value() / (float)sampleRate.Value()));
}

inline TFrequency FFTBinToFrequency(TFFTBin bin, TFFTBin numBins, TSamples sampleRate)
{
    // frequency = bin * SampleRate / numBins
    return TFrequency((float)bin.Value() * (float)sampleRate.Value() / (float)numBins.Value());
}

inline TRadians DegreesToRadians(TDegrees degrees)
{
    return TRadians(degrees.Value() * c_pi / 180.0f);
}

inline TDegrees RadiansToDegrees(TRadians radians)
{
    return TDegrees(radians.Value() * 180.0f / c_pi);
}

inline TDecibels AmplitudeToDB(TAmplitude volume)
{
    return TDecibels(20.0f * log10(volume.Value()));
}
  
inline TAmplitude DBToAmplitude(TDecibels dB)
{
    return TAmplitude(pow(10.0f, dB.Value() / 20.0f));
}

TTimeS SamplesToSeconds(const SSoundSettings &s, TSamples samples)
{
    return TTimeS(samples.Divide(s.m_sampleRate));
}
  
TSamples SecondsToSamples(const SSoundSettings &s, TTimeS seconds)
{
    return TSamples((int)(seconds.Value() * (float)s.m_sampleRate.Value()));
}
  
TSamples MilliSecondsToSamples(const SSoundSettings &s, TTimeMs milliseconds)
{
    return SecondsToSamples(s, TTimeS((float)milliseconds.Value() / 1000.0f));
}
  
TTimeMs SecondsToMilliseconds(TTimeS seconds)
{
    return TTimeMs((uint32)(seconds.Value() * 1000.0f));
}
  
TFrequency Frequency(float octave, float note)
{
    /* frequency = 440×(2^(n/12))
    Notes:
    0  = A
    1  = A#
    2  = B
    3  = C
    4  = C#
    5  = D
    6  = D#
    7  = E
    8  = F
    9  = F#
    10 = G
    11 = G# */
    return TFrequency((float)(440 * pow(2.0, ((double)((octave - 4) * 12 + note)) / 12.0)));
}
  
template 
T AmplitudeToAudioSample(const TAmplitude& in)
{
    const T c_min = std::numeric_limits::min();
    const T c_max = std::numeric_limits::max();
    const float c_minFloat = (float)c_min;
    const float c_maxFloat = (float)c_max;
  
    float ret = in.Value() * c_maxFloat;
  
    if (ret  c_maxFloat)
        return c_max;
  
    return (T)ret;
}

//=====================================================================================
// Audio Utils
//=====================================================================================

void EnvelopeSamples(std::vector& samples, TSamples envelopeTimeFrontBack)
{
    const TSamples c_frontEnvelopeEnd(envelopeTimeFrontBack);
    const TSamples c_backEnvelopeStart(samples.size() - envelopeTimeFrontBack.Value());

    for (TSamples index(0), numSamples(samples.size()); index < numSamples; ++index)
    {
        // calculate envelope
        TAmplitude envelope(1.0f);
        if (index < c_frontEnvelopeEnd)
            envelope = TAmplitude(index.Divide(envelopeTimeFrontBack));
        else if (index > c_backEnvelopeStart)
            envelope = TAmplitude(1.0f) - TAmplitude((index - c_backEnvelopeStart).Divide(envelopeTimeFrontBack));

        // apply envelope
        samples[index.Value()] *= envelope;
    }
}
  
void NormalizeSamples(std::vector& samples, TAmplitude maxAmplitude)
{
    // nothing to do if no samples
    if (samples.size() == 0)
        return;
  
    // 1) find the largest absolute value in the samples.
    TAmplitude largestAbsVal = TAmplitude(abs(samples.front().Value()));
    std::for_each(samples.begin() + 1, samples.end(), [&largestAbsVal](const TAmplitude &a)
        {
            TAmplitude absVal = TAmplitude(abs(a.Value()));
            if (absVal > largestAbsVal)
                largestAbsVal = absVal;
        }
    );
  
    // 2) adjust largestAbsVal so that when we divide all samples, none will be bigger than maxAmplitude
    // if the value we are going to divide by is <= 0, bail out
    largestAbsVal /= maxAmplitude;
    if (largestAbsVal <= TAmplitude(0.0f))
        return;
  
    // 3) divide all numbers by the largest absolute value seen so all samples are [-maxAmplitude,+maxAmplitude]
    for (TSamples index(0), numSamples(samples.size()); index < numSamples; ++index)
        samples[index.Value()] = samples[index.Value()] / largestAbsVal;
}

//=====================================================================================
// Wave File Writing Code
//=====================================================================================
struct SMinimalWaveFileHeader
{
    //the main chunk
    unsigned char m_szChunkID[4];      //0
    uint32        m_nChunkSize;        //4
    unsigned char m_szFormat[4];       //8
  
    //sub chunk 1 "fmt "
    unsigned char m_szSubChunk1ID[4];  //12
    uint32        m_nSubChunk1Size;    //16
    uint16        m_nAudioFormat;      //18
    uint16        m_nNumChannels;      //20
    uint32        m_nSampleRate;       //24
    uint32        m_nByteRate;         //28
    uint16        m_nBlockAlign;       //30
    uint16        m_nBitsPerSample;    //32
  
    //sub chunk 2 "data"
    unsigned char m_szSubChunk2ID[4];  //36
    uint32        m_nSubChunk2Size;    //40
  
    //then comes the data!
};
  
//this writes a wave file
template 
bool WriteWaveFile(const char *fileName, const std::vector &samples, const SSoundSettings &sound)
{
    //open the file if we can
    FILE *file = fopen(fileName, "w+b");
    if (!file)
        return false;
  
    //calculate bits per sample and the data size
    const int32 bitsPerSample = sizeof(T) * 8;
    const int dataSize = samples.size() * sizeof(T);
  
    SMinimalWaveFileHeader waveHeader;
  
    //fill out the main chunk
    memcpy(waveHeader.m_szChunkID, "RIFF", 4);
    waveHeader.m_nChunkSize = dataSize + 36;
    memcpy(waveHeader.m_szFormat, "WAVE", 4);
  
    //fill out sub chunk 1 "fmt "
    memcpy(waveHeader.m_szSubChunk1ID, "fmt ", 4);
    waveHeader.m_nSubChunk1Size = 16;
    waveHeader.m_nAudioFormat = 1;
    waveHeader.m_nNumChannels = 1;
    waveHeader.m_nSampleRate = sound.m_sampleRate.Value();
    waveHeader.m_nByteRate = sound.m_sampleRate.Value() * 1 * bitsPerSample / 8;
    waveHeader.m_nBlockAlign = 1 * bitsPerSample / 8;
    waveHeader.m_nBitsPerSample = bitsPerSample;
  
    //fill out sub chunk 2 "data"
    memcpy(waveHeader.m_szSubChunk2ID, "data", 4);
    waveHeader.m_nSubChunk2Size = dataSize;
  
    //write the header
    fwrite(&waveHeader, sizeof(SMinimalWaveFileHeader), 1, file);
  
    //write the wave data itself, converting it from float to the type specified
    std::vector outSamples;
    outSamples.resize(samples.size());
    for (size_t index = 0; index < samples.size(); ++index)
        outSamples[index] = AmplitudeToAudioSample(samples[index]);
    fwrite(&outSamples[0], dataSize, 1, file);
  
    //close the file and return success
    fclose(file);
    return true;
}

//=====================================================================================
// FFT / IFFT
//=====================================================================================

// Thanks RosettaCode.org!
// http://rosettacode.org/wiki/Fast_Fourier_transform#C.2B.2B
// In production you'd probably want a non recursive algorithm, but this works fine for us

// for use with FFT and IFFT
typedef std::complex Complex;
typedef std::valarray CArray;

// Cooley–Tukey FFT (in-place)
void fft(CArray& x)
{
    const size_t N = x.size();
    if (N <= 1) return;
 
    // divide
    CArray even = x[std::slice(0, N/2, 2)];
    CArray  odd = x[std::slice(1, N/2, 2)];
 
    // conquer
    fft(even);
    fft(odd);
 
    // combine
    for (size_t k = 0; k < N/2; ++k)
    {
        Complex t = std::polar(1.0f, -2 * c_pi * k / N) * odd[k];
        x[k    ] = even[k] + t;
        x[k+N/2] = even[k] - t;
    }
}
 
// inverse fft (in-place)
void ifft(CArray& x)
{
    // conjugate the complex numbers
    x = x.apply(std::conj);
 
    // forward fft
    fft( x );
 
    // conjugate the complex numbers again
    x = x.apply(std::conj);
 
    // scale the numbers
    x /= (float)x.size();
}

//=====================================================================================
// Wave forms
//=====================================================================================

void SineWave(CArray &frequencies, TFFTBin bin, TRadians startingPhase)
{
    // set up the single harmonic
    frequencies[bin.Value()] = std::polar(1.0f, startingPhase.Value());
}

void SawWave(CArray &frequencies, TFFTBin bin, TRadians startingPhase)
{
    // set up each harmonic
    const float volumeAdjustment = 2.0f / c_pi;
    const size_t bucketWalk = bin.Value();
    for (size_t harmonic = 1, bucket = bin.Value(); bucket < frequencies.size() / 2; ++harmonic, bucket += bucketWalk)
        frequencies[bucket] = std::polar(volumeAdjustment / (float)harmonic, startingPhase.Value());
}

void SquareWave(CArray &frequencies, TFFTBin bin, TRadians startingPhase)
{
    // set up each harmonic
    const float volumeAdjustment = 4.0f / c_pi;
    const size_t bucketWalk = bin.Value() * 2;
    for (size_t harmonic = 1, bucket = bin.Value(); bucket < frequencies.size() / 2; harmonic += 2, bucket += bucketWalk)
        frequencies[bucket] = std::polar(volumeAdjustment / (float)harmonic, startingPhase.Value());
}

void TriangleWave(CArray &frequencies, TFFTBin bin, TRadians startingPhase)
{
    // set up each harmonic
    const float volumeAdjustment = 8.0f / (c_pi*c_pi);
    const size_t bucketWalk = bin.Value() * 2;
    for (size_t harmonic = 1, bucket = bin.Value(); bucket < frequencies.size() / 2; harmonic += 2, bucket += bucketWalk, startingPhase *= TRadians(-1.0f))
        frequencies[bucket] = std::polar(volumeAdjustment / ((float)harmonic*(float)harmonic), startingPhase.Value());
}

void NoiseWave(CArray &frequencies, TFFTBin bin, TRadians startingPhase)
{
    // give a random amplitude and phase to each frequency
    for (size_t bucket = 0; bucket < frequencies.size() / 2; ++bucket)
    {
        float amplitude = static_cast  (rand()) / static_cast  (RAND_MAX);
        float phase = 2.0f * c_pi * static_cast  (rand()) / static_cast  (RAND_MAX);
        frequencies[bucket] = std::polar(amplitude, phase);
    }
}

//=====================================================================================
// Tests
//=====================================================================================

template 
void ConsantBins(
    const W &waveForm,
    TFrequency &frequency,
    bool repeat,
    const char *fileName,
    bool normalize,
    TAmplitude multiplier,
    TRadians startingPhase = DegreesToRadians(TDegrees(270.0f))
)
{
    const TFFTBin c_numBins(4096);

    //our desired sound parameters
    SSoundSettings sound;
    sound.m_sampleRate = TSamples(44100);
    sound.m_sampleCount = MilliSecondsToSamples(sound, TTimeMs(500));

    // allocate space for the output file and initialize it
    std::vector samples;
    samples.resize(sound.m_sampleCount.Value());
    std::fill(samples.begin(), samples.end(), TAmplitude(0.0f));

    // make test data
    CArray data(c_numBins.Value());
    waveForm(data, FrequencyToFFTBin(frequency, c_numBins, sound.m_sampleRate), startingPhase);

    // inverse fft - convert from frequency domain (frequencies) to time domain (samples)
    // need to scale up amplitude before fft
    data *= (float)data.size();
    ifft(data);

    // convert to samples
    if (repeat)
    {
        //repeat results in the output buffer
        size_t dataSize = data.size();
        for (size_t i = 0; i < samples.size(); ++i)
            samples[i] = TAmplitude((float)data[i%dataSize].real());
    }
    else
    {
        //put results in the output buffer once.  Useful for debugging / visualization
        for (size_t i = 0; i < samples.size() && i < data.size(); ++i)
            samples[i] = TAmplitude((float)data[i].real());
    }

    // normalize our samples if we should
    if (normalize)
        NormalizeSamples(samples, DBToAmplitude(TDecibels(-3.0f)));

    // apply the multiplier passed in
    std::for_each(samples.begin(), samples.end(), [&](TAmplitude& amplitude) {
        amplitude *= multiplier;
    });

    // write the wave file
    WriteWaveFile(fileName, samples, sound);
}

void Convolve_Circular(const std::vector& a, const std::vector& b, std::vector& result)
{
    // NOTE: Written for readability, not efficiency
    TSamples ASize(a.size());
    TSamples BSize(b.size());

    // NOTE: the circular convolution result doesn't have to be the size of a, i just chose this size to match the ifft
    // circular convolution output.
    result.resize(ASize.Value());
    std::fill(result.begin(), result.end(), TAmplitude(0.0f));

    for (TSamples outputSampleIndex(0), numOutputSamples(ASize); outputSampleIndex < numOutputSamples; ++outputSampleIndex)
    {
        TAmplitude &outputSample = result[outputSampleIndex.Value()];
        for (TSamples sampleIndex(0), numSamples(ASize); sampleIndex < numSamples; ++sampleIndex)
        {
            TSamples BIndex = (outputSampleIndex + ASize - sampleIndex) % ASize;
            if (BIndex < BSize)
            {
                const TAmplitude &ASample = a[sampleIndex.Value()];
                const TAmplitude &BSample = b[BIndex.Value()];
                outputSample += BSample * ASample;
            }
        }
    }
}

void Convolve_Linear(const std::vector& a, const std::vector& b, std::vector& result)
{
    // NOTE: Written for readability, not efficiency
    TSamples ASize(a.size());
    TSamples BSize(b.size());

    result.resize(ASize.Value() + BSize.Value() - 1);
    std::fill(result.begin(), result.end(), TAmplitude(0.0f));

    for (TSamples outputSampleIndex(0), numOutputSamples(result.size()); outputSampleIndex < numOutputSamples; ++outputSampleIndex)
    {
        TAmplitude &outputSample = result[outputSampleIndex.Value()];
        for (TSamples sampleIndex(0), numSamples(ASize); sampleIndex = sampleIndex)
            {
                TSamples BIndex = outputSampleIndex - sampleIndex;
                if (BIndex < BSize)
                {
                    const TAmplitude &ASample = a[sampleIndex.Value()];
                    const TAmplitude &BSample = b[BIndex.Value()];
                    outputSample += BSample * ASample;
                }
            }
        }
    }
}


template 
void DoConvolution(const W1 &waveForm1, const W2 &waveForm2)
{
    const TFFTBin c_numBins(4096);

    //our desired sound parameters
    SSoundSettings sound;
    sound.m_sampleRate = TSamples(44100);
    sound.m_sampleCount = TSamples(c_numBins.Value());

    // make the frequency data for wave form 1
    CArray data1(c_numBins.Value());
    waveForm1(data1, TFFTBin(1), DegreesToRadians(TDegrees(270.0f)));

    // make the frequency data for wave form 2
    CArray data2(c_numBins.Value());
    waveForm2(data2, TFFTBin(1), DegreesToRadians(TDegrees(270.0f)));

    // do circular convolution in time domain by doing multiplication in the frequency domain
    CArray data3(c_numBins.Value());
    data3 = data1 * data2;

    // write out the first convolution input (in time domain samples)
    std::vector samples1;
    samples1.resize(sound.m_sampleCount.Value());
    std::fill(samples1.begin(), samples1.end(), TAmplitude(0.0f));
    {
        data1 *= (float)data1.size();
        ifft(data1);

        // convert to samples
        for (size_t i = 0; i < samples1.size() && i < data1.size(); ++i)
            samples1[i] = TAmplitude((float)data1[i].real());

        // write the wave file
        WriteWaveFile("_convolution_A.wav", samples1, sound);
    }

    // write out the second convolution input (in time domain samples)
    std::vector samples2;
    samples2.resize(sound.m_sampleCount.Value());
    std::fill(samples2.begin(), samples2.end(), TAmplitude(0.0f));
    {
        data2 *= (float)data2.size();
        ifft(data2);

        // convert to samples
        for (size_t i = 0; i < samples2.size() && i < data2.size(); ++i)
            samples2[i] = TAmplitude((float)data2[i].real());

        // write the wave file
        WriteWaveFile("_convolution_B.wav", samples2, sound);
    }

    // write the result of the convolution (in time domain samples)
    {
        data3 *= (float)data3.size();
        ifft(data3);

        // convert to samples
        std::vector samples3;
        samples3.resize(sound.m_sampleCount.Value());
        for (size_t i = 0; i < samples3.size() && i < data3.size(); ++i)
            samples3[i] = TAmplitude((float)data3[i].real());

        // write the wave file
        NormalizeSamples(samples3, TAmplitude(1.0f));
        WriteWaveFile("_convolution_out_ifft.wav", samples3, sound);
    }

    // do linear convolution in the time domain and write out the wave file
    {
        std::vector samples4;
        Convolve_Linear(samples1, samples2, samples4);
        NormalizeSamples(samples4, TAmplitude(1.0f));
        WriteWaveFile("_convolution_out_lin.wav", samples4, sound);
    }

    // do circular convolution in time domain and write out the wave file
    {
        std::vector samples4;
        Convolve_Circular(samples1, samples2, samples4);
        NormalizeSamples(samples4, TAmplitude(1.0f));
        WriteWaveFile("_convolution_out_cir.wav", samples4, sound);
    }
}

//=====================================================================================
// Frequency Over Time Track Structs
//=====================================================================================

struct SBinTrack
{
    SBinTrack() { }

    SBinTrack(
        TFFTBin bin,
        std::function amplitudeFunction,
        TRadians phase = DegreesToRadians(TDegrees(270.0f))
    )
        : m_bin(bin)
        , m_amplitudeFunction(amplitudeFunction)
        , m_phase(phase) {}

    TFFTBin                                     m_bin;
    std::function   m_amplitudeFunction;
    TRadians                                    m_phase;
};

//=====================================================================================
// Frequency Amplitude Over Time Test
//=====================================================================================

void TracksToSamples_IFFT_Window(const std::vector &tracks, CArray &windowData, TTimeS time, TTimeS totalTime)
{
    // clear out the window data
    windowData = Complex(0.0f, 0.0f);

    // gather the bin data
    std::for_each(tracks.begin(), tracks.end(), [&](const SBinTrack &track) {
        windowData[track.m_bin.Value()] = std::polar(track.m_amplitudeFunction(time, totalTime).Value(), track.m_phase.Value());
    });

    // convert it to time samples
    windowData *= (float)windowData.size();
    ifft(windowData);
}

void TracksToSamples_IFFT(const std::vector &tracks, std::vector &samples, TTimeS totalTime, TFFTBin numBins)
{
    // convert the tracks to samples, one window of numBins at a time
    CArray windowData(numBins.Value());
    for (TSamples startSample(0), numSamples(samples.size()); startSample < numSamples; startSample += TSamples(numBins.Value()))
    {
        // Convert the tracks that we can into time samples using ifft
        float percent = startSample.Divide(numSamples);
        TTimeS time(totalTime.Value() * percent);
        TracksToSamples_IFFT_Window(tracks, windowData, time, totalTime);

        // convert window data to samples
        const size_t numWindowSamples = std::min(numBins.Value(), (numSamples - startSample).Value());
        for (size_t i = 0; i < numWindowSamples; ++i)
            samples[startSample.Value() + i] = TAmplitude((float)windowData[i].real());
    }
}

void TracksToSamples_Oscilators(const std::vector &tracks, std::vector &samples, TTimeS totalTime, TFFTBin numBins)
{
    // Render each time/amplitude track in each frequency bin to actual cosine samples
    float samplesPerSecond = (float)samples.size() / totalTime.Value();
    float ratio = samplesPerSecond / (float)numBins.Value();
    for (size_t i = 0, c = samples.size(); i < c; ++i)
    {
        float percent = (float)i / (float)c;
        TTimeS time(totalTime.Value() * percent);
        samples[i].Value() = 0.0f;
        std::for_each(tracks.begin(), tracks.end(),
            [&](const SBinTrack &track)
            {
                TAmplitude amplitude = track.m_amplitudeFunction(time, totalTime);
                samples[i] += TAmplitude(cos(time.Value()*c_twoPi*ratio*(float)track.m_bin.Value() + track.m_phase.Value())) * amplitude;
            }
        );
    }
}

struct SFadePair
{
    TTimeS m_time;
    TAmplitude m_amplitude;
};

std::function MakeFadeFunction(std::initializer_list fadePairs)
{
    // if no faid pairs, 0 amplitude always
    if (fadePairs.size() == 0)
    {
        return [](TTimeS time, TTimeS totalTime) -> TAmplitude
        {
            return TAmplitude(0.0f);
        };
    }

    // otherwise, use the fade info to make an amplitude over time track
    // NOTE: assume amplitude 0 at time 0 and totalTime
    return [fadePairs](TTimeS time, TTimeS totalTime) -> TAmplitude
    {
        TTimeS lastFadeTime(0.0f);
        TAmplitude lastFadeAmplitude(0.0f);

        for (size_t i = 0; i < fadePairs.size(); ++i)
        {
            if (time < fadePairs.begin()[i].m_time)
            {
                TAmplitude percent(((time - lastFadeTime) / (fadePairs.begin()[i].m_time - lastFadeTime)).Value());
                return percent * (fadePairs.begin()[i].m_amplitude - lastFadeAmplitude) + lastFadeAmplitude;
            }
            lastFadeTime = fadePairs.begin()[i].m_time;
            lastFadeAmplitude = fadePairs.begin()[i].m_amplitude;
        }
        if (time < totalTime)
        {
            TAmplitude percent(((time - lastFadeTime) / (totalTime - lastFadeTime)).Value());
            return percent * (TAmplitude(0.0f) - lastFadeAmplitude) + lastFadeAmplitude;
        }

        return TAmplitude(0.0f);
    };
}

void DynamicBins(TFFTBin numBins, const std::vector& tracks, const char *fileNameFFT, const char * fileNameOsc)
{
    //our desired sound parameters
    SSoundSettings sound;
    sound.m_sampleRate = TSamples(44100);
    sound.m_sampleCount = MilliSecondsToSamples(sound, TTimeMs(2000));

    // allocate space for the output file and initialize it
    std::vector samples;
    samples.resize(sound.m_sampleCount.Value());
    std::fill(samples.begin(), samples.end(), TAmplitude(0.0f));

    const TTimeS totalTime = SamplesToSeconds(sound, sound.m_sampleCount);

    // convert our frequency over time descriptions to time domain samples using IFFT
    if (fileNameFFT)
    {
        TracksToSamples_IFFT(tracks, samples, totalTime, numBins);
        NormalizeSamples(samples, DBToAmplitude(TDecibels(-3.0f)));
        EnvelopeSamples(samples, MilliSecondsToSamples(sound, TTimeMs(50)));
        WriteWaveFile(fileNameFFT, samples, sound);
    }

    // convert our frequency over time descriptions to time domain samples using Oscillators
    // and additive synthesis
    if (fileNameOsc)
    {
        TracksToSamples_Oscilators(tracks, samples, totalTime, numBins);
        NormalizeSamples(samples, DBToAmplitude(TDecibels(-3.0f)));
        EnvelopeSamples(samples, MilliSecondsToSamples(sound, TTimeMs(50)));
        WriteWaveFile(fileNameOsc, samples, sound);
    }
}

//=====================================================================================
// Main
//=====================================================================================
int main(int argc, char **argv)
{
     // make some basic wave forms with IFFT
    ConsantBins(NoiseWave, Frequency(3, 8), true, "_noise.wav", true, TAmplitude(1.0f));
    ConsantBins(SquareWave, Frequency(3, 8), true, "_square.wav", true, TAmplitude(1.0f));
    ConsantBins(TriangleWave, Frequency(3, 8), true, "_triangle.wav", true, TAmplitude(1.0f));
    ConsantBins(SawWave, Frequency(3, 8), true, "_saw.wav", true, TAmplitude(1.0f));
    ConsantBins(SineWave, Frequency(3, 8), true, "_cosine.wav", true, TAmplitude(1.0f), TRadians(0.0f));
    ConsantBins(SineWave, Frequency(3, 8), true, "_sine.wav", true, TAmplitude(1.0f));

    // show saw wave phase shifted.  Looks different but sounds the same!
    // You can do the same with square, saw, triangle (and other more complex wave forms)
    // We take the saw waves down 12 db though because some variations have large peaks so would clip otherwise.
    // we don't normalize because we want you to hear them all at the same loudness to tell that they really do sound the same.
    ConsantBins(SawWave, Frequency(3, 8), true, "_saw_0.wav"  , false, DBToAmplitude(TDecibels(-12.0f)), DegreesToRadians(TDegrees(0.0f)));
    ConsantBins(SawWave, Frequency(3, 8), true, "_saw_15.wav" , false, DBToAmplitude(TDecibels(-12.0f)), DegreesToRadians(TDegrees(15.0f)));
    ConsantBins(SawWave, Frequency(3, 8), true, "_saw_30.wav" , false, DBToAmplitude(TDecibels(-12.0f)), DegreesToRadians(TDegrees(30.0f)));
    ConsantBins(SawWave, Frequency(3, 8), true, "_saw_45.wav" , false, DBToAmplitude(TDecibels(-12.0f)), DegreesToRadians(TDegrees(45.0f)));
    ConsantBins(SawWave, Frequency(3, 8), true, "_saw_60.wav" , false, DBToAmplitude(TDecibels(-12.0f)), DegreesToRadians(TDegrees(60.0f)));
    ConsantBins(SawWave, Frequency(3, 8), true, "_saw_75.wav" , false, DBToAmplitude(TDecibels(-12.0f)), DegreesToRadians(TDegrees(75.0f)));
    ConsantBins(SawWave, Frequency(3, 8), true, "_saw_90.wav" , false, DBToAmplitude(TDecibels(-12.0f)), DegreesToRadians(TDegrees(90.0f)));
    ConsantBins(SawWave, Frequency(3, 8), true, "_saw_105.wav", false, DBToAmplitude(TDecibels(-12.0f)), DegreesToRadians(TDegrees(105.0f)));
    ConsantBins(SawWave, Frequency(3, 8), true, "_saw_120.wav", false, DBToAmplitude(TDecibels(-12.0f)), DegreesToRadians(TDegrees(120.0f)));
    ConsantBins(SawWave, Frequency(3, 8), true, "_saw_135.wav", false, DBToAmplitude(TDecibels(-12.0f)), DegreesToRadians(TDegrees(135.0f)));
    ConsantBins(SawWave, Frequency(3, 8), true, "_saw_150.wav", false, DBToAmplitude(TDecibels(-12.0f)), DegreesToRadians(TDegrees(150.0f)));
    ConsantBins(SawWave, Frequency(3, 8), true, "_saw_165.wav", false, DBToAmplitude(TDecibels(-12.0f)), DegreesToRadians(TDegrees(165.0f)));
    ConsantBins(SawWave, Frequency(3, 8), true, "_saw_180.wav", false, DBToAmplitude(TDecibels(-12.0f)), DegreesToRadians(TDegrees(180.0f)));
    ConsantBins(SawWave, Frequency(3, 8), true, "_saw_270.wav", false, DBToAmplitude(TDecibels(-12.0f)), DegreesToRadians(TDegrees(270.0f)));

    // show how IFFT can have popping at window edges
    {
        std::vector tracks;
        tracks.emplace_back(SBinTrack(TFFTBin(10), [](TTimeS time, TTimeS totalTime) -> TAmplitude
        {
            return TAmplitude(cos(time.Value()*c_twoPi*4.0f) * 0.5f + 0.5f);
        }));

        // make a version that starts at a phase of 0 degrees and has popping at the
        // edges of each IFFT window
        tracks.front().m_phase = TRadians(0.0f);
        DynamicBins(TFFTBin(1024), tracks, "_IFFTTest1.wav", nullptr);

        // make a version that starts at a phase of 270 degrees and is smooth at the
        // edges of each IFFT window but can only change amplitude at the edges of
        // each window.
        tracks.front().m_phase = TRadians(DegreesToRadians(TDegrees(270.0f)));
        DynamicBins(TFFTBin(1024), tracks, "_IFFTTest2.wav", nullptr);

        // make a version with oscillators and additive synthesis which has no
        // popping and can also change amplitude anywhere in the wave form.
        DynamicBins(TFFTBin(1024), tracks, nullptr, "_IFFTTest3.wav");
    }

    // make an alien sound using both IFFT and oscillators (additive synthesis)
    {
        std::vector tracks;
        tracks.emplace_back(SBinTrack(TFFTBin(1), MakeFadeFunction({ { TTimeS(0.5f), TAmplitude(1.0f) }, { TTimeS(1.0f), TAmplitude(0.5f) } })));
        tracks.emplace_back(SBinTrack(TFFTBin(2), MakeFadeFunction({ { TTimeS(1.0f), TAmplitude(1.0f) } })));
        tracks.emplace_back(SBinTrack(TFFTBin(3), MakeFadeFunction({ { TTimeS(1.5f), TAmplitude(1.0f) } })));
        tracks.emplace_back(SBinTrack(TFFTBin(5), MakeFadeFunction({ { TTimeS(1.25f), TAmplitude(1.0f) } })));
        tracks.emplace_back(SBinTrack(TFFTBin(10), [](TTimeS time, TTimeS totalTime) -> TAmplitude
        {
            float value = (cos(time.Value()*c_twoPi*4.0f) * 0.5f + 0.5f) * 0.5f;
            if (time < totalTime * TTimeS(0.5f))
                value *= (time / (totalTime*TTimeS(0.5f))).Value();
            else
                value *= 1.0f - ((time - totalTime*TTimeS(0.5f)) / (totalTime*TTimeS(0.5f))).Value();
            return TAmplitude(value);
        }));
        DynamicBins(TFFTBin(1024), tracks, "_alien_ifft.wav", "_alien_osc.wav");
    }

    // Make some drum beats
    {
        // frequency = bin * SampleRate / numBins
        // frequency = bin * 44100 / 4096
        // frequency ~= bin * 10.75
        // up to 22050hz at bin 2048

        TFFTBin c_numBins(4096);
        TSamples c_sampleRate(44100);

        std::vector tracks;

        const TTimeS timeMultiplier(1.1f);

        // base drum: 100-200hz every half second
        {
            const TFFTBin start(FrequencyToFFTBin(TFrequency(100.0f), c_numBins, c_sampleRate));
            const TFFTBin end(FrequencyToFFTBin(TFrequency(200.0f), c_numBins, c_sampleRate));
            const TFFTBin step(5);

            auto beat = [&](TTimeS time, TTimeS totalTime)->TAmplitude
            {
                time *= timeMultiplier;
                time = TTimeS(std::fmod(time.Value(), 0.5f));
                const TTimeS attack(0.01f);
                const TTimeS release(TTimeS(0.2f) - attack);
                const TTimeS totalBeatTime(attack + release);

                TAmplitude ret;
                if (time < attack)
                    ret = TAmplitude(time.Divide(attack));
                else if (time < totalBeatTime)
                    ret = TAmplitude(1.0f) - TAmplitude((time - attack).Divide(release));
                else
                    ret = TAmplitude(0.0f);
                return ret * TAmplitude(10.0f);
            };
            for (TFFTBin i = start; i TAmplitude
            {
                time *= timeMultiplier;
                time = TTimeS(std::fmod(time.Value() + 0.25f, 1.0f));
                const TTimeS attack(0.025f);
                const TTimeS release(TTimeS(0.075f) - attack);
                const TTimeS totalBeatTime(attack + release);

                TAmplitude ret;
                if (time < attack)
                    ret = TAmplitude(time.Divide(attack));
                else if (time < totalBeatTime)
                    ret = TAmplitude(1.0f) - TAmplitude((time - attack).Divide(release));
                else
                    ret = TAmplitude(0.0f);
                return ret;
            };
            for (TFFTBin i = start; i TAmplitude
            {
                time *= timeMultiplier;
                time = TTimeS(std::fmod(time.Value() + 0.75f, 1.0f));
                const TTimeS attack(0.025f);
                const TTimeS release(TTimeS(0.075f) - attack);
                const TTimeS totalBeatTime(attack + release);

                TAmplitude ret;
                if (time < attack)
                    ret = TAmplitude(time.Divide(attack));
                else if (time < totalBeatTime)
                    ret = TAmplitude(1.0f) - TAmplitude((time - attack).Divide(release));
                else
                    ret = TAmplitude(0.0f);
                return ret;
            };
            for (TFFTBin i = start; i <= end; i += step)
                tracks.emplace_back(SBinTrack(i, beat));
        }

        // render the result with both ifft and oscillators
        DynamicBins(c_numBins, tracks, "_drums_ifft.wav", "_drums_osc.wav");
    }

    // do our convolution tests
    DoConvolution(SawWave, SquareWave);

    return 0;
}

Links

So, frequency domain audio synthesis with IFFT is kind of a mixed bag. It can be good so long as you are ok with it’s limitations, but if you aren’t, it’s better to stick to oscillators and do additive synthesis.

Working in the frequency domain in general is pretty cool though. If you bust out a spectrograph and analyze the frequency of a type of sound, once you understand the frequency domain makeup of that sound, you can go back and synthesize it yourself using either oscillators or IFFT. You can go down this route to make your own synth guitar sound, or trumpet, or you could try to mimic sound effects. The world is your oyster! Well, almost… things like “voice synthesis” are actually pretty complex, and this method for matching musical instruments will only get you so far. More to come in future posts!

Here are some links to dive a bit deeper into this stuff:

I think I might be burned out on audio for a while, my thoughts are turning towards graphics so look for some graphics posts soon 😛

Decibels (dB) and Amplitude

If you are a programmer, chances are that when you think of volume or volume adjustments of audio signals (or other streams of data), you are thinking in terms of amplitude.

For instance, to make an audio stream quieter, you are probably going to multiply all the samples by 0.5 to bring it down in volume. That 0.5 is a scalar value in amplitude space.

If you work with musicians or other audio folk, chances are they are not going to think in amplitude, may not be able to easily adjust to thinking in amplitude, and instead will talk to you in terms of decibels or dB, which is as foreign to you as amplitude is to them.

The main issue is that our ears do not hear linear adjustments in amplitude as linear adjustments in loudness, but linear adjustments in dB do sound like they are linear adjustments in loudness.

dB is a bit easier to understand as well. 0dB means full volume and positive numbers means a boost in volume, while negative numbers mean a decrease in volume.

dB combines linearly, unlike amplitudes which have to multiply together. -6db means that the volume has been cut in half, and -12db means that it has been cut in half again (so is 1/4 as loud) and -18db means that it has been cut in half yet again (now 1/8 as loud). Doing the same with amplitude, 0.5 means that the volume is cut in half, and then you multiply that by 0.5 to get 0.25 to make it 1/4 as loud, and multiply again to get 0.125 which is 1/8 as loud.

A fun byproduct of this is that using dB you can never describe zero (silence) exactly. People will usually adopt a convention of saying that below -60dB is silence, or below -96dB is silence. This has a nice side benefit that you can make the cutoff point of “assumed silence” be above the level that floating point denormals are (very small numbers that need special processing and are slower to work with than regular floating point numbers), so that in effect you can use this to remove denormals from your processing, which can boost the performance of your code.

Conversion Functions

To convert from amplitude to dB, the formula is:

dB = 20 * log10(amplitude)

To convert from dB to amplitude, the formula is:

amplitude = 10^(db/20)

Note that when converting audio samples to dB, you want to take the absolute value of the audio sample, since sign doesn’t matter for loudness. -1 and +1 have the same loudness (0dB).

Here’s some c++ code which does those two operations:

inline float AmplitudeTodB(float amplitude)
{
  return 20.0f * log10(amplitude);
}

inline float dBToAmplitude(float dB)
{
  return pow(10.0f, db/20.0f);
}

Conversion Table

Here are some dB values and corresponding amplitude values to help you better understand how dB and amplitude are related.

Decreasing Volume:

dB	Amplitude
-1	0.891
-3	0.708
-6	0.501
-12	0.251
-18	0.126
-20	0.1
-40	0.01
-60	0.001
-96	0.00002

Increasing Volume:

dB	Amplitude
1	1.122
3	1.413
6	1.995
12	3.981
18	7.943
20	10
40	100
60	1000
96	63095.734

Next Up

I’m just about finished doing the research for a fourier synthesis post to show how to use the inverse fourier transform to turn frequency information into audio samples. Look for that in the next couple days!

DIY Synth: Convolution Reverb & 1D Discrete Convolution of Audio Samples

This is a part of the DIY Synthesizer series of posts where each post is roughly built upon the knowledge of the previous posts. If you are lost, check the earlier posts!

I just learned about this technique a couple weeks ago and am SUPER stoked to be able to share this info. Honestly, it’s kind of bad ass and a little magical.

If there is a physical location that has the reverb you are looking for (a church, a cave, your bathroom, the subway, whatever), you can go there and record the sound of some short, loud sound (a clap, a starter pistol, whatever). Now that you have this sound file, you can use a mathematical technique called “Discrete Convolution” (not as difficult as it sounds) to apply that reverb to other sounds.

Not only that, you can use convolution to apply various properties of one sound to another sound. Like you could convolve a saw wave and a recording of a voice and make it sound robotic.

This is pretty cool right?

Convolution

There are two types of convolution out there… continuous convolution and discrete convolution.

Continuous convolution is a method where you can take two formulas and perform some operations (algebra, calculus, etc) to get a third formula.

In the cases that us programmers usually work with, however, you usually only have data, and not a mathematical formula describing that data.

When you have specific data points instead of an equation, you can use something called discrete convolution instead.

Discrete convolution is a method where you take two streams of data (IE two arrays of data!) and perform some operations (only looping, addition and multiplication!) to get a third stream of data.

Interestingly, this third stream of data will be the size of the first stream of data, plus the size of the second stream of data, minus one.

This link explains discrete convolution much better than I could, and even has an interactive demo, so check it out: Discrete Convolution

Here is some pseudo code that shows how discrete convolution works.

// We are calculating bufferA * bufferB (discrete convolution)
// initialize out buffer to empty, and make sure it's the right size
outBuffer[sizeof(bufferA)+sizeof(bufferB)-1] = 0

// reverse one of the buffers in preperation of the convolution
reverse(bufferB);

// Convolve!
for (int outBufferIndex = 0; outBufferIndex < sizeof(outBuffer); ++outBufferIndex)
{
  bufferAIndex = 0;
  bufferBIndex = 0;
  if (outBufferIndex < sizeof(bufferB))
    bufferBIndex = sizeof(bufferB) - outBufferIndex - 1;
  else
    bufferAIndex = outBufferIndex - sizeof(bufferB);

  for (; bufferAIndex < sizeof(bufferA) && bufferBIndex < sizeof(bufferB); ++bufferAIndex, ++bufferBIndex)
  {
    outBuffer[outBufferIndex] += bufferA[bufferAIndex] * bufferB[bufferBIndex];
  }
}

That's all there is to it!

Convolution Reverb

Like I mentioned above, to do convolution reverb you just convolve the audio file you want to add reverb to with the recorded sound from the place that has the reverb you want. That second sound is called the Impulse Response, or IR for short.

Besides letting you choose a reverb model (like “cavernous” or “small hallway” or “bright tiled room”), many reverbs will have a “wetness” parameter that controls how much reverb you hear versus how much of the origional noise you hear. A wetness of 1.0 means all you hear is the reverb (the convolution), while a wetness of 0.0 means all you hear is the origional sound (the dry sound). It’s just a percentage and literally is just used to lerp between the two signals.

Here is an example of how changes in wetness can sound, and also give you a first glimpse of just how good this technique works!

Dry Sound: SoundBite
Impulse Response: ReverbLarge

Convolved with 100% wetness: c_RL_SBite.wav
Convolved with 66% wetness: c_RL_SBite_66.wav
Convolved with 33% wetness: c_RL_SBite_33.wav

Sample Sound Files

Let’s convolve some sounds together and see what results we get!

Here are 11 sounds convoled against each other (and themselves) at 100% wetness so all you hear is the convolution. Convolution is commutative (A*B == B*A) so that cuts down on the number of combinations (66 instead of 121!)

There are 3 impulse responses, 4 short basic wave forms, 2 voice samples a cymbal drum pattern and a jaw harp twang.

Some of the results are pretty interesting, for instance check out SoundBite vs SoundCymbal. The beat of the cymbal pattern remains, but the actual symbal sound itself is replaced by the words!

	ReverbLarge
ReverbLarge	c_RL_RL.wav
ReverbMedium	c_RL_RM.wav
ReverbSmall	c_RL_RS.wav
SoundBite	c_RL_SBite.wav
SoundCymbal	c_RL_SCymbal.wav
SoundJawharp	c_RL_SJawharp.wav
SoundLegend	c_RL_SLegend.wav
SoundSaw	c_RL_SSaw.wav
SoundSine	c_RL_SSine.wav
SoundSquare	c_RL_SSquare.wav
SoundTriangle	c_RL_STriangle.wav
	ReverbMedium
ReverbLarge	c_RL_RM.wav
ReverbMedium	c_RM_RM.wav
ReverbSmall	c_RM_RS.wav
SoundBite	c_RM_SBite.wav
SoundCymbal	c_RM_SCymbal.wav
SoundJawharp	c_RM_SJawharp.wav
SoundLegend	c_RM_SLegend.wav
SoundSaw	c_RM_SSaw.wav
SoundSine	c_RM_SSine.wav
SoundSquare	c_RM_SSquare.wav
SoundTriangle	c_RM_STriangle.wav
	ReverbSmall
ReverbLarge	c_RL_RS.wav
ReverbMedium	c_RM_RS.wav
ReverbSmall	c_RS_RS.wav
SoundBite	c_RS_SBite.wav
SoundCymbal	c_RS_SCymbal.wav
SoundJawharp	c_RS_SJawharp.wav
SoundLegend	c_RS_SLegend.wav
SoundSaw	c_RS_SSaw.wav
SoundSine	c_RS_SSine.wav
SoundSquare	c_RS_SSquare.wav
SoundTriangle	c_RS_STriangle.wav
	SoundBite
ReverbLarge	c_RL_SBite.wav
ReverbMedium	c_RM_SBite.wav
ReverbSmall	c_RS_SBite.wav
SoundBite	c_SBite_SBite.wav
SoundCymbal	c_SBite_SCymbal.wav
SoundJawharp	c_SBite_SJawharp.wav
SoundLegend	c_SBite_SLegend.wav
SoundSaw	c_SBite_SSaw.wav
SoundSine	c_SBite_SSine.wav
SoundSquare	c_SBite_SSquare.wav
SoundTriangle	c_SBite_STriangle.wav
	SoundCymbal
ReverbLarge	c_RL_SCymbal.wav
ReverbMedium	c_RM_SCymbal.wav
ReverbSmall	c_RS_SCymbal.wav
SoundBite	c_SBite_SCymbal.wav
SoundCymbal	c_SCymbal_SCymbal.wav
SoundJawharp	c_SCymbal_SJawharp.wav
SoundLegend	c_SCymbal_SLegend.wav
SoundSaw	c_SCymbal_SSaw.wav
SoundSine	c_SCymbal_SSine.wav
SoundSquare	c_SCymbal_SSquare.wav
SoundTriangle	c_SCymbal_STriangle.wav
	SoundJawharp
ReverbLarge	c_RL_SJawharp.wav
ReverbMedium	c_RM_SJawharp.wav
ReverbSmall	c_RS_SJawharp.wav
SoundBite	c_SBite_SJawharp.wav
SoundCymbal	c_SCymbal_SJawharp.wav
SoundJawharp	c_SJawharp_SJawharp.wav
SoundLegend	c_SJawharp_SLegend.wav
SoundSaw	c_SJawharp_SSaw.wav
SoundSine	c_SJawharp_SSine.wav
SoundSquare	c_SJawharp_SSquare.wav
SoundTriangle	c_SJawharp_STriangle.wav
	SoundLegend
ReverbLarge	c_RL_SLegend.wav
ReverbMedium	c_RM_SLegend.wav
ReverbSmall	c_RS_SLegend.wav
SoundBite	c_SBite_SLegend.wav
SoundCymbal	c_SCymbal_SLegend.wav
SoundJawharp	c_SJawharp_SLegend.wav
SoundLegend	c_SLegend_SLegend.wav
SoundSaw	c_SLegend_SSaw.wav
SoundSine	c_SLegend_SSine.wav
SoundSquare	c_SLegend_SSquare.wav
SoundTriangle	c_SLegend_STriangle.wav
	SoundSaw
ReverbLarge	c_RL_SSaw.wav
ReverbMedium	c_RM_SSaw.wav
ReverbSmall	c_RS_SSaw.wav
SoundBite	c_SBite_SSaw.wav
SoundCymbal	c_SCymbal_SSaw.wav
SoundJawharp	c_SJawharp_SSaw.wav
SoundLegend	c_SLegend_SSaw.wav
SoundSaw	c_SSaw_SSaw.wav
SoundSine	c_SSaw_SSine.wav
SoundSquare	c_SSaw_SSquare.wav
SoundTriangle	c_SSaw_STriangle.wav
	SoundSine
ReverbLarge	c_RL_SSine.wav
ReverbMedium	c_RM_SSine.wav
ReverbSmall	c_RS_SSine.wav
SoundBite	c_SBite_SSine.wav
SoundCymbal	c_SCymbal_SSine.wav
SoundJawharp	c_SJawharp_SSine.wav
SoundLegend	c_SLegend_SSine.wav
SoundSaw	c_SSaw_SSine.wav
SoundSine	c_SSine_SSine.wav
SoundSquare	c_SSine_SSquare.wav
SoundTriangle	c_SSine_STriangle.wav
	SoundSquare
ReverbLarge	c_RL_SSquare.wav
ReverbMedium	c_RM_SSquare.wav
ReverbSmall	c_RS_SSquare.wav
SoundBite	c_SBite_SSquare.wav
SoundCymbal	c_SCymbal_SSquare.wav
SoundJawharp	c_SJawharp_SSquare.wav
SoundLegend	c_SLegend_SSquare.wav
SoundSaw	c_SSaw_SSquare.wav
SoundSine	c_SSine_SSquare.wav
SoundSquare	c_SSquare_SSquare.wav
SoundTriangle	c_SSquare_STriangle.wav
	SoundTriangle
ReverbLarge	c_RL_STriangle.wav
ReverbMedium	c_RM_STriangle.wav
ReverbSmall	c_RS_STriangle.wav
SoundBite	c_SBite_STriangle.wav
SoundCymbal	c_SCymbal_STriangle.wav
SoundJawharp	c_SJawharp_STriangle.wav
SoundLegend	c_SLegend_STriangle.wav
SoundSaw	c_SSaw_STriangle.wav
SoundSine	c_SSine_STriangle.wav
SoundSquare	c_SSquare_STriangle.wav
SoundTriangle	c_STriangle_STriangle.wav

Sample Code

Here is some sample code which will read in “in.wav” and “reverb.wav”, do convolution on them and save the fully wet result (convolution result only, no original in.wav mixed into the output) as “out.wav”.

Note that this code was used to process the sample sound files above. Usual caveat: The sound loading code isn’t bulletproof. I’ve found it works best with 16 bit mono sound files. If you need better sound loading, check out libsndfile!

#define _CRT_SECURE_NO_WARNINGS
 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
 
#define _USE_MATH_DEFINES
#include 
 
//=====================================================================================
// SNumeric - uses phantom types to enforce type safety
//=====================================================================================
template 
struct SNumeric
{
public:
    explicit SNumeric(const T &value) : m_value(value) { }
    SNumeric() : m_value() { }
    inline T& Value() { return m_value; }
    inline const T& Value() const { return m_value; }
 
    typedef SNumeric TType;
    typedef T TInnerType;
 
    // Math Operations
    TType operator+ (const TType &b) const
    {
        return TType(this->Value() + b.Value());
    }
 
    TType operator- (const TType &b) const
    {
        return TType(this->Value() - b.Value());
    }
 
    TType operator* (const TType &b) const
    {
        return TType(this->Value() * b.Value());
    }
 
    TType operator/ (const TType &b) const
    {
        return TType(this->Value() / b.Value());
    }
 
    TType& operator+= (const TType &b)
    {
        Value() += b.Value();
        return *this;
    }
 
    TType& operator-= (const TType &b)
    {
        Value() -= b.Value();
        return *this;
    }
 
    TType& operator*= (const TType &b)
    {
        Value() *= b.Value();
        return *this;
    }
 
    TType& operator/= (const TType &b)
    {
        Value() /= b.Value();
        return *this;
    }
 
    TType& operator++ ()
    {
        Value()++;
        return *this;
    }
 
    TType& operator-- ()
    {
        Value()--;
        return *this;
    }
 
    // Extended Math Operations
    template 
    T Divide(const TType &b)
    {
        return ((T)this->Value()) / ((T)b.Value());
    }
 
    // Logic Operations
    bool operatorValue() < b.Value();
    }
    bool operatorValue()  (const TType &b) const {
        return this->Value() > b.Value();
    }
    bool operator>= (const TType &b) const {
        return this->Value() >= b.Value();
    }
    bool operator== (const TType &b) const {
        return this->Value() == b.Value();
    }
    bool operator!= (const TType &b) const {
        return this->Value() != b.Value();
    }
 
private:
    T m_value;
};
 
//=====================================================================================
// Typedefs
//=====================================================================================
 
typedef uint8_t uint8;
typedef uint16_t uint16;
typedef uint32_t uint32;
typedef int16_t int16;
typedef int32_t int32;
 
// type safe types!
typedef SNumeric      TFrequency;
typedef SNumeric        TTimeMs;
typedef SNumeric       TSamples;
typedef SNumeric   TFractionalSamples;
typedef SNumeric       TDecibels;
typedef SNumeric      TAmplitude;
typedef SNumeric          TPhase;
 
//=====================================================================================
// Constants
//=====================================================================================
 
static const float c_pi = (float)M_PI;
static const float c_twoPi = c_pi * 2.0f;
 
//=====================================================================================
// Structs
//=====================================================================================
 
struct SSoundSettings
{
    TSamples        m_sampleRate;
};
 
//=====================================================================================
// Conversion Functions
//=====================================================================================
inline TDecibels AmplitudeToDB(TAmplitude volume)
{
    return TDecibels(log10(volume.Value()));
}
 
inline TAmplitude DBToAmplitude(TDecibels dB)
{
    return TAmplitude(pow(10.0f, dB.Value() / 20.0f));
}
 
TSamples SecondsToSamples(const SSoundSettings &s, float seconds)
{
    return TSamples((int)(seconds * (float)s.m_sampleRate.Value()));
}
 
TSamples MilliSecondsToSamples(const SSoundSettings &s, float milliseconds)
{
    return SecondsToSamples(s, milliseconds / 1000.0f);
}
 
TTimeMs SecondsToMilliseconds(float seconds)
{
    return TTimeMs((uint32)(seconds * 1000.0f));
}
 
TFrequency Frequency(float octave, float note)
{
    /* frequency = 440×(2^(n/12))
    Notes:
    0  = A
    1  = A#
    2  = B
    3  = C
    4  = C#
    5  = D
    6  = D#
    7  = E
    8  = F
    9  = F#
    10 = G
    11 = G# */
    return TFrequency((float)(440 * pow(2.0, ((double)((octave - 4) * 12 + note)) / 12.0)));
}
 
template 
T AmplitudeToAudioSample(const TAmplitude& in)
{
    const T c_min = std::numeric_limits::min();
    const T c_max = std::numeric_limits::max();
    const float c_minFloat = (float)c_min;
    const float c_maxFloat = (float)c_max;
 
    float ret = in.Value() * c_maxFloat;
 
    if (ret  c_maxFloat)
        return c_max;
 
    return (T)ret;
}
 
TAmplitude GetLerpedAudioSample(const std::vector& samples, TFractionalSamples& index)
{
    // get the index of each sample and the fractional blend amount
    uint32 a = (uint32)floor(index.Value());
    uint32 b = a + 1;
    float fract = index.Value() - floor(index.Value());
 
    // get our two amplitudes
    float ampA = 0.0f;
    if (a >= 0 && a = 0 && b < samples.size())
        ampB = samples[b].Value();
 
    // return the lerped result
    return TAmplitude(fract * ampB + (1.0f - fract) * ampA);
}
 
void NormalizeSamples(std::vector& samples, TAmplitude maxAmplitude, TSamples envelopeTimeFrontBack)
{
    // nothing to do if no samples
    if (samples.size() == 0)
        return;
 
    // 1) find the largest absolute value in the samples.
    TAmplitude largestAbsVal = TAmplitude(abs(samples.front().Value()));
    std::for_each(samples.begin() + 1, samples.end(), [&largestAbsVal](const TAmplitude &a)
        {
            TAmplitude absVal = TAmplitude(abs(a.Value()));
            if (absVal > largestAbsVal)
                largestAbsVal = absVal;
        }
    );
 
    // 2) adjust largestAbsVal so that when we divide all samples, none will be bigger than maxAmplitude
    // if the value we are going to divide by is <= 0, bail out
    largestAbsVal /= maxAmplitude;
    if (largestAbsVal <= TAmplitude(0.0f))
        return;
 
    // 3) divide all numbers by the largest absolute value seen so all samples are [-maxAmplitude,+maxAmplitude]
    // also apply front and back envelope
    const TSamples c_frontEnvelopeEnd(envelopeTimeFrontBack);
    const TSamples c_backEnvelopeStart(samples.size() - envelopeTimeFrontBack.Value());

    for (TSamples index(0), numSamples(samples.size()); index < numSamples; ++index)
    {
        // calculate envelope
        TAmplitude envelope(1.0f);
        if (index < c_frontEnvelopeEnd)
            envelope = TAmplitude(index.Divide(envelopeTimeFrontBack));
        else if (index > c_backEnvelopeStart)
            envelope = TAmplitude(1.0f) - TAmplitude((index - c_backEnvelopeStart).Divide(envelopeTimeFrontBack));

        // apply envelope while normalizing
        samples[index.Value()] = samples[index.Value()] * envelope / largestAbsVal;

    }
}
 
void ResampleData(std::vector& samples, int srcSampleRate, int destSampleRate)
{
    //if the requested sample rate is the sample rate it already is, bail out and do nothing
    if (srcSampleRate == destSampleRate)
        return;
 
    //calculate the ratio of the old sample rate to the new
    float fResampleRatio = (float)destSampleRate / (float)srcSampleRate;
 
    //calculate how many samples the new data will have and allocate the new sample data
    int nNewDataNumSamples = (int)((float)samples.size() * fResampleRatio);
 
    std::vector newSamples;
    newSamples.resize(nNewDataNumSamples);
 
    //get each lerped output sample.  There are higher quality ways to resample
    for (int nIndex = 0; nIndex < nNewDataNumSamples; ++nIndex)
        newSamples[nIndex] = GetLerpedAudioSample(samples, TFractionalSamples((float)nIndex / fResampleRatio));
 
    //free the old data and set the new data
    std::swap(samples, newSamples);
}
 
void ChangeNumChannels(std::vector& samples, int nSrcChannels, int nDestChannels)
{
    //if the number of channels requested is the number of channels already there, or either number of channels is not mono or stereo, return
    if (nSrcChannels == nDestChannels ||
        nSrcChannels  2 ||
        nDestChannels  2)
    {
        return;
    }
 
    //if converting from mono to stereo, duplicate the mono channel to make stereo
    if (nDestChannels == 2)
    {
        std::vector newSamples;
        newSamples.resize(samples.size() * 2);
        for (size_t index = 0; index < samples.size(); ++index)
        {
            newSamples[index * 2] = samples[index];
            newSamples[index * 2 + 1] = samples[index];
        }
 
        std::swap(samples, newSamples);
    }
    //else converting from stereo to mono, mix the stereo channels together to make mono
    else
    {
        std::vector newSamples;
        newSamples.resize(samples.size() / 2);
        for (size_t index = 0; index < samples.size() / 2; ++index)
            newSamples[index] = samples[index * 2] + samples[index * 2 + 1];
 
        std::swap(samples, newSamples);
    }
}
 
float PCMToFloat(unsigned char *pPCMData, int nNumBytes)
{
    switch (nNumBytes)
    {
    case 1:
    {
        uint8 data = pPCMData[0];
        return (float)data / 255.0f;
    }
    case 2:
    {
        int16 data = pPCMData[1] << 8 | pPCMData[0];
        return ((float)data) / ((float)0x00007fff);
    }
    case 3:
    {
        int32 data = pPCMData[2] << 16 | pPCMData[1] << 8 | pPCMData[0];
        return ((float)data) / ((float)0x007fffff);
    }
    case 4:
    {
        int32 data = pPCMData[3] << 24 | pPCMData[2] << 16 | pPCMData[1] << 8 | pPCMData[0];
        return ((float)data) / ((float)0x7fffffff);
    }
    default:
    {
        return 0.0f;
    }
    }
}
 
//=====================================================================================
// Wave File Writing Code
//=====================================================================================
struct SMinimalWaveFileHeader
{
    //the main chunk
    unsigned char m_szChunkID[4];      //0
    uint32        m_nChunkSize;        //4
    unsigned char m_szFormat[4];       //8
 
    //sub chunk 1 "fmt "
    unsigned char m_szSubChunk1ID[4];  //12
    uint32        m_nSubChunk1Size;    //16
    uint16        m_nAudioFormat;      //18
    uint16        m_nNumChannels;      //20
    uint32        m_nSampleRate;       //24
    uint32        m_nByteRate;         //28
    uint16        m_nBlockAlign;       //30
    uint16        m_nBitsPerSample;    //32
 
    //sub chunk 2 "data"
    unsigned char m_szSubChunk2ID[4];  //36
    uint32        m_nSubChunk2Size;    //40
 
    //then comes the data!
};
 
//this writes a wave file
template 
bool WriteWaveFile(const char *fileName, const std::vector &samples, const SSoundSettings &sound)
{
    //open the file if we can
    FILE *file = fopen(fileName, "w+b");
    if (!file)
        return false;
 
    //calculate bits per sample and the data size
    const int32 bitsPerSample = sizeof(T) * 8;
    const int dataSize = samples.size() * sizeof(T);
 
    SMinimalWaveFileHeader waveHeader;
 
    //fill out the main chunk
    memcpy(waveHeader.m_szChunkID, "RIFF", 4);
    waveHeader.m_nChunkSize = dataSize + 36;
    memcpy(waveHeader.m_szFormat, "WAVE", 4);
 
    //fill out sub chunk 1 "fmt "
    memcpy(waveHeader.m_szSubChunk1ID, "fmt ", 4);
    waveHeader.m_nSubChunk1Size = 16;
    waveHeader.m_nAudioFormat = 1;
    waveHeader.m_nNumChannels = 1;
    waveHeader.m_nSampleRate = sound.m_sampleRate.Value();
    waveHeader.m_nByteRate = sound.m_sampleRate.Value() * 1 * bitsPerSample / 8;
    waveHeader.m_nBlockAlign = 1 * bitsPerSample / 8;
    waveHeader.m_nBitsPerSample = bitsPerSample;
 
    //fill out sub chunk 2 "data"
    memcpy(waveHeader.m_szSubChunk2ID, "data", 4);
    waveHeader.m_nSubChunk2Size = dataSize;
 
    //write the header
    fwrite(&waveHeader, sizeof(SMinimalWaveFileHeader), 1, file);
 
    //write the wave data itself, converting it from float to the type specified
    std::vector outSamples;
    outSamples.resize(samples.size());
    for (size_t index = 0; index < samples.size(); ++index)
        outSamples[index] = AmplitudeToAudioSample(samples[index]);
    fwrite(&outSamples[0], dataSize, 1, file);
 
    //close the file and return success
    fclose(file);
    return true;
}
 
//loads a wave file in.  Converts from source format into the specified format
// TOTAL HONESTY: some wave files seem to have problems being loaded through this function and I don't have
// time to investigate why.  It seems to work best with 16 bit mono wave files.
// If you need more robust file loading, check out libsndfile at http://www.mega-nerd.com/libsndfile/
bool ReadWaveFile(const char *fileName, std::vector& samples, int32 sampleRate)
{
    //open the file if we can
    FILE *File = fopen(fileName, "rb");
    if (!File)
    {
        return false;
    }
 
    //read the main chunk ID and make sure it's "RIFF"
    char buffer[5];
    buffer[4] = 0;
    if (fread(buffer, 4, 1, File) != 1 || strcmp(buffer, "RIFF"))
    {
        fclose(File);
        return false;
    }
 
    //read the main chunk size
    uint32 nChunkSize;
    if (fread(&nChunkSize, 4, 1, File) != 1)
    {
        fclose(File);
        return false;
    }
 
    //read the format and make sure it's "WAVE"
    if (fread(buffer, 4, 1, File) != 1 || strcmp(buffer, "WAVE"))
    {
        fclose(File);
        return false;
    }
 
    long chunkPosFmt = -1;
    long chunkPosData = -1;
 
    while (chunkPosFmt == -1 || chunkPosData == -1)
    {
        //read a sub chunk id and a chunk size if we can
        if (fread(buffer, 4, 1, File) != 1 || fread(&nChunkSize, 4, 1, File) != 1)
        {
            fclose(File);
            return false;
        }
 
        //if we hit a fmt
        if (!strcmp(buffer, "fmt "))
        {
            chunkPosFmt = ftell(File) - 8;
        }
        //else if we hit a data
        else if (!strcmp(buffer, "data"))
        {
            chunkPosData = ftell(File) - 8;
        }
 
        //skip to the next chunk
        fseek(File, nChunkSize, SEEK_CUR);
    }
 
    //we'll use this handy struct to load in 
    SMinimalWaveFileHeader waveData;
 
    //load the fmt part if we can
    fseek(File, chunkPosFmt, SEEK_SET);
    if (fread(&waveData.m_szSubChunk1ID, 24, 1, File) != 1)
    {
        fclose(File);
        return false;
    }
 
    //load the data part if we can
    fseek(File, chunkPosData, SEEK_SET);
    if (fread(&waveData.m_szSubChunk2ID, 8, 1, File) != 1)
    {
        fclose(File);
        return false;
    }
 
    //verify a couple things about the file data
    if (waveData.m_nAudioFormat != 1 ||       //only pcm data
        waveData.m_nNumChannels  2 ||        //must not have more than 2
        waveData.m_nBitsPerSample > 32 ||     //32 bits per sample max
        waveData.m_nBitsPerSample % 8 != 0 || //must be a multiple of 8 bites
        waveData.m_nBlockAlign > 8)           //blocks must be 8 bytes or lower
    {
        fclose(File);
        return false;
    }
 
    //figure out how many samples and blocks there are total in the source data
    int nBytesPerBlock = waveData.m_nBlockAlign;
    int nNumBlocks = waveData.m_nSubChunk2Size / nBytesPerBlock;
    int nNumSourceSamples = nNumBlocks * waveData.m_nNumChannels;
 
    //allocate space for the source samples
    samples.resize(nNumSourceSamples);
 
    //maximum size of a block is 8 bytes.  4 bytes per samples, 2 channels
    unsigned char pBlockData[8];
    memset(pBlockData, 0, 8);
 
    //read in the source samples at whatever sample rate / number of channels it might be in
    int nBytesPerSample = nBytesPerBlock / waveData.m_nNumChannels;
    for (int nIndex = 0; nIndex = TPhase(1.0f))
        phase -= TPhase(1.0f);
    while (phase  0.5f ? 1.0f : -1.0f);
}
 
TAmplitude AdvanceOscilator_Triangle(TPhase &phase, TFrequency frequency, TSamples sampleRate)
{
    AdvancePhase(phase, frequency, sampleRate);
    if (phase > TPhase(0.5f))
        return TAmplitude((((1.0f - phase.Value()) * 2.0f) * 2.0f) - 1.0f);
    else
        return TAmplitude(((phase.Value() * 2.0f) * 2.0f) - 1.0f);
}
 
TAmplitude AdvanceOscilator_Saw_BandLimited(TPhase &phase, TFrequency frequency, TSamples sampleRate)
{
    AdvancePhase(phase, frequency, sampleRate);
 
    // sum the harmonics
    TAmplitude ret(0.0f);
    for (int harmonicIndex = 1; harmonicIndex <= 4; ++harmonicIndex)
    {
        TPhase harmonicPhase = phase * TPhase((float)harmonicIndex);
        ret += TAmplitude(sin(harmonicPhase.Value()*c_twoPi) / (float)harmonicIndex);
    }
 
    //adjust the volume
    ret *= TAmplitude(2.0f / c_pi);
 
    return ret;
}
 
TAmplitude AdvanceOscilator_Square_BandLimited(TPhase &phase, TFrequency frequency, TSamples sampleRate)
{
    AdvancePhase(phase, frequency, sampleRate);
 
    // sum the harmonics
    TAmplitude ret(0.0f);
    for (int harmonicIndex = 1; harmonicIndex <= 4; ++harmonicIndex)
    {
        float harmonicFactor = (float)harmonicIndex * 2.0f - 1.0f;
        TPhase harmonicPhase = phase * TPhase(harmonicFactor);
        ret += TAmplitude(sin(harmonicPhase.Value()*c_twoPi) / harmonicFactor);
    }
 
    //adjust the volume
    ret *= TAmplitude(4.0f / c_pi);
 
    return ret;
}
 
TAmplitude AdvanceOscilator_Triangle_BandLimited(TPhase &phase, TFrequency frequency, TSamples sampleRate)
{
    AdvancePhase(phase, frequency, sampleRate);
 
    // sum the harmonics
    TAmplitude ret(0.0f);
    TAmplitude signFlip(1.0f);
    for (int harmonicIndex = 1; harmonicIndex <= 4; ++harmonicIndex)
    {
        float harmonicFactor = (float)harmonicIndex * 2.0f - 1.0f;
        TPhase harmonicPhase = phase * TPhase(harmonicFactor);
        ret += TAmplitude(sin(harmonicPhase.Value()*c_twoPi) / (harmonicFactor*harmonicFactor)) * signFlip;
        signFlip *= TAmplitude(-1.0f);
    }
 
    //adjust the volume
    ret *= TAmplitude(8.0f / (c_pi*c_pi));
 
    return ret;
}
 
//=====================================================================================
// Main
//=====================================================================================
int main(int argc, char **argv)
{
    // wetness parameter of reverb.  It's a percentage from 0 to 1.  
    TAmplitude c_reverbWetness(1.0f);

    // keep track of when the process started so we can report how long it took
    auto start = std::chrono::system_clock::now().time_since_epoch();

    //our desired sound parameters
    SSoundSettings sound;
    sound.m_sampleRate = TSamples(44100);
 
    // load the input wave file if we can and normalize it
    std::vector inputData;
    if (!ReadWaveFile("in.wav", inputData, sound.m_sampleRate.Value()))
    {
        printf("could not load input wave file!");
        return 0;
    }
    NormalizeSamples(inputData, TAmplitude(1.0f), TSamples(0));

    // load the reverb wave file if we can and normalize it
    std::vector reverbData;
    if (!ReadWaveFile("reverb.wav", reverbData, sound.m_sampleRate.Value()))
    {
        printf("could not load reverb wave file!");
        return 0;
    }
    NormalizeSamples(reverbData, TAmplitude(1.0f), TSamples(0));

    // allocate space for the output file - which will be the number of samples in the two input files minus 1
    // initialize it to silence!
    std::vector samples;
    samples.resize(inputData.size() + reverbData.size() - 1);
    std::fill(samples.begin(), samples.end(), TAmplitude(0.0f));

    // reverse the reverb data in preparation of convolution
    std::reverse(reverbData.begin(), reverbData.end());

    // report the number of samples of each file
    printf("Input samples = %un", inputData.size());
    printf("Reverb samples = %un", reverbData.size());

    // apply the convolution for each output sample
    float lastPercentageReported = 0.0f;
    char percentageText[512];
    percentageText[0] = 0;
    printf("Progress: ");
    for (TSamples sampleIndex(0), numSamples(samples.size()); sampleIndex < numSamples; ++sampleIndex)
    {
        // print some periodic output since this can take a while!
        float percentage = sampleIndex.Divide(numSamples);
        if (percentage >= lastPercentageReported + 0.01f)
        {
            // erase the last progress text
            for (int i = 0, c = strlen(percentageText); i < c; ++i)
                printf("%c %c", 8, 8);

            // calculte and show progress text
            lastPercentageReported = percentage;
            auto duration = std::chrono::system_clock::now().time_since_epoch() - start;
            auto millis = std::chrono::duration_cast(duration).count();
            float expectedMillis = millis / percentage;
            sprintf(percentageText, "%i%%  %0.2f / %0.2f seconds (%0.2f remaining)", int(percentage*100.0f), ((float)millis) / 1000.0f, expectedMillis / 1000.0f, (expectedMillis - millis) / 1000.0f);
            printf("%s", percentageText);
        }

        // get a reference to our output sample
        TAmplitude &outputSample = samples[sampleIndex.Value()];

        // figure out the first reverb index and input index we should process.
        TSamples startReverbIndex(0);
        TSamples startInputIndex(0);
        if (sampleIndex < TSamples(reverbData.size()))
            startReverbIndex = TSamples(reverbData.size()) - sampleIndex - TSamples(1);
        else
            startInputIndex = sampleIndex - TSamples(reverbData.size());

        // for each reverb sample
        for (TSamples reverbIndex(startReverbIndex), numReverbSamples(reverbData.size()), inputIndex(startInputIndex), numInputSamples(inputData.size());
            reverbIndex < numReverbSamples && inputIndex < numInputSamples;
            ++reverbIndex, ++inputIndex)
        {
            const TAmplitude &inputSample = inputData[inputIndex.Value()];
            const TAmplitude &reverbSample = reverbData[reverbIndex.Value()];
            outputSample += inputSample * reverbSample;
        }
    }

    // normalize the reverb to the wetness volume level
    NormalizeSamples(samples, c_reverbWetness, TSamples(0));

    // apply the dry sound on top, per the wetness settings
    for (TSamples inputIndex = TSamples(0), numInputSamples(inputData.size()); inputIndex < numInputSamples; ++inputIndex)
    {
        const TAmplitude &inputSample = inputData[inputIndex.Value()];
        TAmplitude &outputSample = samples[inputIndex.Value()];
        outputSample += inputSample * (TAmplitude(1.0f) - c_reverbWetness);
    }

    // normalize the amplitude of the samples to make sure they are as loud as possible without clipping.
    // give 3db of headroom and also put an envelope on the front and back that is 50ms
    NormalizeSamples(samples, DBToAmplitude(TDecibels(-3.0f)), MilliSecondsToSamples(sound, 50.0f));
 
    // save as a wave file
    WriteWaveFile("out.wav", samples, sound);
    return 0;
}

Intuition

I had to think about it for a bit but the intuition for why this works is actually pretty straight forward!

The impulse response represents all the echos that occur over time if you make a single sample of 1.0 amplitude. This is your guide for how all samples in an impulse source (IS) should be transformed, where IS is the sound you want to add reverb to.

So, starting out, you put the entire IR into your output buffer starting at output[0] (the first sample in the output buffer), multiplied by IS[0] (the first sample of the sound you are reverbing).

This leaves you with the proper reverb of the first sample in your IS, and your total output buffer length is the same length as your IR.

We only have one sample reverbed though, so we move to the next…

Next, you put the entire IR into the output buffer again, but this time start at output[1] (the second sample in the output buffer) and those IR values you are writing need to be multiplied by IS[1] (the second sample of the sound you are reverbing).

You now have the proper reverb for the first two samples in your IS, and your total output buffer length is the length of your IR + 1.

Rinse and repeat for all samples in your IS, and at the end, the reverb of all samples in your IS will be accounted for in your output buffer, and the size of your output buffer will be the length of your IR plus the length of your IS, minus one.

Pretty simple and intuitive right?

You are essentially playing the IR in the output buffer length(IS) times, where IS[outputBufferIndex] determines the volume (amplitude) that you need to play the IR at.

Convolution does exactly this, which turns out to be pretty slow due to it being a lot of math to preform.

If you have a source file (IS) you are reverbing that is 4 seconds long, running at 44100 samples per second (176,400 samples total), and you have a reverb impulse response (IR) that is 2 seconds long at 44100 samples per second (88,200 samples total), that means that you are going to essentially be mixing the IR into an output buffer 176,400 times.

Each time you play the IR you need to do a multiplication per IR sample (to scale it to the IS[index] amplitude) and an addition to add it to the resulting output buffer.

At 88,200 IR samples with a multiply and add for each sample, and doing that 176,400 times, that means at the end you will need to do 15,558,480,000 (15.5 billion) multiplies and adds.

And remember… that is only for a 4 second sound that is receiving a 2 second reverb… those are pretty small sound files involved! And, that is only a single channel. That would double in stereo, and be even worse in 5.1 or 7.1 surround sound!

More Info

So, this method works, but unfortunately it’s pretty darn slow (it took like 5 minutes for me to convolve the legend quote with the large reverb). It could be made faster by introducing threading and SSE instructions, but there is a better way that gives us an even bigger speed up.

Having audio samples means you are working in the “time domain”. If you take a fourier transform of the audio samples, you’ll have the information in the “frequency domain”. As it turns out, if you do a multiplication in the frequency domain, that is equivalent to doing a convolution in the time domain. Using the fast fourier transform on your input sound and multiplying that by the pre-transformed FFT of the impulse response, and then doing an inverse FFT on the result to get back into the time domain (aka audio samples) is MUCH FASTER than doing actual convolution.

Another problem with convolution reverb is that you need the full sound you are convolving, which makes it basically impossible to use in a live setup. The solution to this is that people convolve windows of data at a time, instead of the whole sound. I think a common window size is 256 samples.

I’ll make a post in the future that addresses both those issues to allow for fast, real time convolution reverb via windowed FFT multiplication.

Also, I said in the last post that this technique is what the pros do. We’ll I should add that this is what they do SOMETIMES. Other times they use DSP algorithms involving comb filters and multi tap delays (and other things) to make fast reverb that sounds pretty decent without needing to do convolution or FFT/IFFT. Check the links section for a link to the details of one such algorithm.

Regarding IR samples (Impulse Response recordings), if you record your own, it should work as is. However, a common thing that people do is remove the loud sound from the impulse response (via deconvolution i think?) to get ONLY the impulse response. It basically makes it so that the IR really is just an IR of that room as if you had a single sample of a “1.0” echoing in the area. Without this step, your reverb convolution will still work, but you’ll get “smearing” of the sound, due to it not being a true 1.0 sample (or in other words, not a true dirac delta).

Luckily there are IR’s available for download online as well. Some are free, some are pay. Check the links section for a few links I found for that (:

Lastly, this post basically teaches you how to do 1 dimensional convolution, showing you an application for it. You can do convolution in higher dimensions as well though, and in fact if you have used photoshop and know about things like gaussian blur, sharpen mask, etc, those guys work by 2d convolution. Bokeh is even apparently convolution, as is a “Minkowski Sum” if you have done work in game physics.

Ill make a graphics related 2d convolution post in the future as well to delve into that stuff a bit deeper.

As one final sound sample, check out this CROSS CORRELATION (not convolution) of SoundBite.wav and ReverbLarge. Cross correlation is the same as convolution except you don’t reverse one of the samples. So, in effect, it’s like I convolved SoundBite.wav with ReverbLarge.wav played backwards.

c_ReverseRL_SBite.wav

More info on cross correlation coming soon. It has uses in audio, but more often it’s used for finding time delays of sounds compared to other sounds, recognizing patterns in sound data even with the presence of noise / distortion, versus having actual audible uses (although there are some of those too!).

Links

A good read explaining 1d and 2d convolution
More info on convolution reverb
Even more info on convolution reverb
Explains discrete convolution and has an interactive demo
Khan Academy: Continuous Convolution
Info on faked reverb
More info on faked reverb
A reverb blog!
Some free IRs you can download

HyperLogLog: Estimate Unique Value Counts Like The Pros

This is the last of my planned posts on probabilistic algorithms. There may be more in the future, but the initial volley is finished 😛

Thanks again to Ben Deane for exposure to this really interesting area of computer science.

This post is about HyperLogLog, which is used to estimate a count of how many “uniques” there are in a stream of data. It can also do intersection and union between two hyperloglog objects allowing you to see how many items HLL objects have in common. It was invented in 2007 and is currently used in many big data situations including use by Google and Redis and Amazon.

This algorithm is probabilistic in that you can trade storage space for accuracy. You can calculate how much accuracy to expect for a given amount of storage, or calculate how much storage you’d need for a specific amount of accuracy.

If this sounds a lot like the first probabilistic algorithm post I made (Estimating Counts of Distinct Values with KMV) that means you have been paying attention. HyperLogLog is in the same family of algorithms, but it is way better at most things than KMV is, and seems to be the current standard for DV Sketches (distinct value estimators). The one thing KMV seems to be better at is calculating intersections between objects, which i’ll talk about more below.

To give you an idea of the power of HyperLogLog, here’s a quote from the paper it was first described in (link at end of post):

“…the new algorithm makes it possible to estimate cardinalities well beyond 10^9 with a typical accuracy of 2% while using a memory of only 1.5 kilobytes”

By the end of this post you should understand how that is possible, and also be able to start with the sample code and have HyperLogLog capabilities in your own C++ project immediately!

A Usage Case: Upvoting

A usage case for this algorithm would be adding an “upvote” button to a webpage.

A naive solution to this would be to have an upvote button that when clicked would increment a counter on the server. That is problematic though because people can vote as many times as they want. You could hack together a solution to this by having some client side cookies and javascript limiting people from doing that, but all your security is out the window since it’s a client side fix, and you will soon have trolls spamming your vote counters by doing raw HTTP requests to your servers, to ruin your day, just because they can.

A less naive solution would be to have some unique identifier per user – whether that was something like a username, or just an IP address – and store that in a voting table, only allowing the counter to increment if the person wasn’t already in the table, and entering them into the table when doing the increment.

The problem with that solution is that the table of users who have already voted might get extremely huge, causing lots of memory usage to hold it, lots of processing time to see if a user exists in the table already (even with a hash based lookup), and it doesn’t parallelize very well to multiple servers. You also have to implement some protection against race conditions around the “look for user in table, increment vote counter, add user to table” work, which means some potentially costly synchronization logic.

A better solution would be to use HyperLogLog and Here are some reasons why:

It has a fixed size you determine in advance. The bold quote from the paper would indicate that 1.5KB is likely enough for our needs, being able to count over one billion unique values. Bringing it up to 2KB would be enough to store a heck of a lot more, like somewhere up near 2^250 unique items.
It automatically disallows the same item being accounted for more than once, so our multiple votes from same voter problem is gone with no need for costly synchronization work.
It lends itself well to being parallelized across machines, or just using SIMD / GPGPU if you wanted to squeeze some more performance out of it.
You can very quickly do set operations on multiple HLL objects.

The first three items solve the problems in the naive solutions, but the fourth adds some bonus functionality that is pretty cool.

Using set operations, you can do things like figure out if the same people are upvoting a dulce de leche flan desert compared to a cheesy grits recipe, and you can calculate that VERY QUICKLY.

A possibly naive way to suggest a recipe to a user would be to show them recipes that a lot of people have upvoted.

A more custom tailored suggestion (and thus, hopefully a better suggestion) would be when a person votes on a recipe, you can tell them “hey, a lot of the same people that upvoted the recipe you just upvoted also upvoted this other recipe, why don’t you check it out!”

So now, you don’t just have a voting system, you now also have a CLASSIFICATION SYSTEM.

Yeah ok, so that’s a little hand wavy and making a real suggestion system has more details to solve than just those etc etc, but hopefully you can see how this algorithm can be a fundamental building block to many “big data” problems.

Onto the details of how it works!

Basic Premise – Coin Flips

When you flip a coin, what are the odds that it will be heads? There’s even chance of heads or tails, so the chance of a heads is 1 in 2 or 1/2 or 50%.

What are the odds that if you flip a coin twice it a row it will be heads both times? Well, on each flip there is a 50% chance, so you multiply .5 * .5 to get the answer which is .25 or 25%. There’s a 25% chance, or a 1 in 4 chance, that you will flip heads twice in a row with two coin flips. It’s the same chance that you will flip two tails in a row, or that you will flip heads then tails, or tails then heads. All possible outcomes have the same probability.

Another way to look at this, instead of probability, is to see how many combinations possible there are like this:

Sequence Number	Sequence
0	heads, heads
1	heads, tails
2	tails, heads
3	tails, tails

There’s a 100% chance that two coin flips will be somewhere in those four results, and all results have an even chance of happening, so result 0 “heads, heads” has a 1 in 4 chance of happening. All of the results above have a 1 in 4 chance. Interestingly, looking at the above table you can also see that there is a 2/4 chance that the first flip will be heads, which is also 1/2, 1 in 2 or 50% chance. That agrees with what we said before, that if only doing one coin flip (the first coin flip), there is a 50% chance of heads or tails.

If you switched to 3 coin flips, there would be a 1 in 8 chance of any specific event happening, since there are 8 possible outcomes:

Sequence Number	Sequence
0	heads, heads, heads
1	heads, heads, tails
2	heads, tails, heads
3	heads, tails, tails
4	tails, heads, heads
5	tails, heads, tails
6	tails, tails, heads
7	tails, tails, tails

It doesn’t matter which specific sequence you are looking at above, the chance that 3 coin flips will result in any of those specific sequences is 1 in 8.

In fact, for N coin flips, the probability that you will encounter any specific sequence (permutation) of heads and tails is 1 in 2^N, or 1/(2^N).

Now, let’s change it up a bit. What are the odds that you will have some number of heads in a row, and then a tails? In other words, what are the odds that you will have a “run” of heads of a specified length?

well, a run of 0 would just be you flip the coin once and get tails. Since you are doing one coin flip and you are looking for a specific one of two possible outcomes to happen, the probability is or 1 in 2, or 1/2, or 50%.

A run of 1 would mean you flipped the coin once, got heads, flipped it again and got tails. Since you are doing two coin flips and are looking for a specific one of four possible outcomes, the probability of that happening is 1/2*1/2 = 1/4, or 1 in 4, or 25%.

A run of 2 means heads, heads, tails. 3 coin flips = 1/2*1/2*1/2 = 1/8, or 1 in 8, or 12.5%.

By now you may have noticed that the probability for getting N heads and then a tail is just 1 in the number of coin flips, and the number of coin flips is 2^(N+1).

More formally, the odds of getting N heads and then a tail is 1/(2^(N+1)).

Let’s now swap out the idea of heads and tails with the idea of binary digits 0 and 1 in a sequence of random numbers. Think of “heads” as 0, and “tails” as 1.

If you generate a random bit (binary digit), there is a 50% chance it will be a 0, and a 50% chance it will be a 1.

If you generate two random bits, there is a 25% chance for each of the possible outcomes below:

Sequence Number	Sequence
0	00
1	01
2	10
3	11

Now, what are the odds that in a random binary number, we will have N zeros and then a 1?

Don’t let the binary digits scare you, it’s the same answer as the coin flip question: 1/(2^(N+1))

An interesting property of this is that if you ask for a random 8 bit binary number and get xxxxx100, using the formula above, you know there is a 1 in 8 chance that a random number would end in “100”.

Using this information you can say to yourself “i’ll bet I’ve seen about 8 different random numbers at this point”, and that’s a fairly decent guess, without actually having had to pay attention to any of the numbers that came before.

A better idea though would be to watch all the random numbers as they are generated, and keep track the longest run of zeros you’ve seen on the right side of any number.

Using this “longest run seen” value, you can guess how many unique random numbers you’ve seen so far. If the longest run you’ve seen is N zeros and then a 1, the guess as to how many random numbers you’ve seen is 2^(N+1).

If you’ve seen a maximum of 4 zeros and a 1 (xxx10000), you’ve probably seen about 32 numbers on average. If you’ve seen at maximum 2 zeros and a 1 (xxxxx100), you’ve probably seen about 8 numbers on average.

Since by definition, randomness is RANDOM, there will be fluctuation and your guess will not always be so accurate. You might have only seen one random number, but it’s value may have been 10000000 (0x80), which would incorrectly cause you to estimate that 256 items have been seen (2^8), when in fact only a single item has been seen.

To combat this, HyperLogLog uses multiple registers (counters) to keep multiple counts, and then averages the estimates together. More info on that below, but for now, hopefully you can see how that would smooth things out towards a more average case. The more registers you use, the more “average case” your estimation should be, so the more accurate your estimate should be.

There’s an interesting twist here though… you aren’t actually estimating how many random numbers you’ve seen, but instead are estimating how many UNIQUE random numbers you’ve seen. Random numbers can repeat, but this count estimation will only count each unique value once, no matter how many times it appears.

To help visualize that, no matter how many times you see 10110100 – whether it’s only once, or ten thousand times – the longest run will still be 2. After you’ve seen ten thousand of those numbers, as soon as you see the next number 10011000, the longest run will then be 3.

That may sound like a trivial difference that we are counting uniques, and not actual values, but as the next section will show, it’s actually a very important difference, and is where this technique derives it’s power.

Also, if we were counting non uniques, we could just use an integer and increment it for each item we saw (;

Hashing Functions as Pseudorandom Number Generators

An interesting property of good hashing algorithms is that the output you get when you hash an object will be indistinguishable from random numbers. If you hash 3, you’ll get a random number, and if you hash 4, you’ll likely get a completely different random number. You can’t tell from the output what the nature of the input was, or how similar the input objects were.

But, of course, when you put the same input into a hash function, you will always get the same output.

These two properties are what makes hash functions so useful in what we are trying to do in HLL.

Quick Tangent: These same properties also apply to encryption by the way. The fact that they are random output is why hashed and encrypted data doesn’t compress very well. There are no patterns in the data that can be exploited to express the data as anything shorter than the full length of data itself. You should not be able to gain any knowledge about the nature of the input by looking at the output, except perhaps the size of the source data in the case of encryption. Also, whereas hashes are not reversible at all, encryption is only reversible if you have the encryption key (password). HLL and similar algorithms use hashes, not encryption, because they want a fixed size output, and they don’t care about reversing the process.

The output of the hash function is the source of the pseudorandom numbers that we plug into the HyperLogLog algorithm, and is what allows us to count uniques of any type of thing, so long as that thing can be hashed.

So, to do HLL counting, you hash every object you see in a stream keeping track of the longest run of zeros (in binary) you’ve seen in the resulting hashes. You store “longest runs seen” in multiple registers which you can then later use to get an averaged estimate of unique items encountered. That’s all there is to it.

MAGIC!

That’s how things work from a high level, now let’s get into the nitty gritty a bit…

Handling Multiple Registers

Let’s say you have a hash function that spits out a 32 bit hash, which is a pretty common thing for HLL implementations.

We talked about figuring out the length of the run of 0’s in the hash output, but if you had 16 registers to store run lengths in, how do you choose which register to store each run length in?

The common way to solve this is to use some of your hash bits for register selection. If you have 16 registers, you could use the lowest 4 bits of your hash as the register index to store the count in for instance.

There is a problem here though, that hopefully you can see already. The problem is that if we have a run of 3 with a hash that ends in the binary number 1000, we will only ever store that run length in register 8! By using the same bits for register selection as we do for counting numbers, we’ve biased our count and introduced inaccuracy (error) because certain numbers will only get accounted for by specific registers. The ideal situation is that every number is as likely to end up in any specific register versus another one. It should “randomly” choose what register to use, but be deterministic in how it chose that register.

The bits you use for register selection cannot be reused for counting runs, or else you’ll fall into the trap of only storing certain numbers in specific registers.

You could perhaps hash your hash to get another pseudo random number to use for register selection, but a better option is to just throw out those register selection bits once you use them.

Reducing the number of bits you evaluate for runs of 0’s comes at a cost though. It means that your estimation of unique values seen is capped at a lower number. with 32 bits, you can estimate a count up to 2^32 (~4 billion), but at 28 bits, after using 4 bits for register selection, you can only estimate a count of up to 2^28 (~268 million).

I believe this is one of the reasons why google invented “HyperLogLog++” which uses a 64 bit hash and has some other improvements. Check the links at the bottom of this post for more information.

It’s a bit overkill, but in the sample code in this post, we create a 128 bit hash, use the top 32 bits for register selection, and the lower 96 bits for looking at runs. I say it’s overkill because at 96 bits, we can estimate counts up to 79 billion billion billion, which is way huger than anyone (even google!) is ever likely to need.

Register Sizes

As I mentioned above, many people use 32 bit hashes, for estimating at most about 4 billion unique objects. Google bumps it up to 64 bits for up to 18 billion billion uniques, and our sample code uses 96 bits for run evaluation, letting us estimate counts up to 79 billion billion billion.

These numbers are beyond huge, but believe it or not, the size of the registers themselves used to track these things are pretty darn tiny.

Since we are looking for runs of zeros, if we have a 32 bit hash, we only need to be able to store the values 0 to 32. 0 to 31 can be stored in 5 bits, and chances are that people aren’t going to bump it up to 6 bits just to get that extra value – especially when in practice you are going to use a few bits of the hash as register selection.

So, for a 32 bit hash, you really only need 5 bits per register to keep track of longest runs seen.

For a 64 bit hash, you need to be able to store the values 0 to 64. Similar to the above, 0-63 can be stored in 6 bits, and we can ditch being able to store 64, so 6 bits per register is plenty.

For our 96 bit hash (since we use 32 bits for register selection), we’d only need to be able to store 0-96, which can fit entirely in 7 bits, since 7 bits can store 0-127.

In our example code, I’m an excessive glutton however, and store our longest run value in 8 bits, wasting an entire bit of memory per register.

Yep, in our excessively gigantic counting 128 bit hash HLL DV Sketch code, i use an ENTIRE BYTE of memory per register. The Horror!!!

With a 32 or 64 bit hash, you could drop that down to 5 or 6 bits per register, and either condense your registers in memory, or perhaps even use those extra bits for something else if you wanted (need some flags?!).

Register Counts

So, our register size itself is fairly tiny, where my gluttonous, wasteful programming uses a single byte per register. How many registers do we need though?

The answer to that depends on how much accuracy you want.

To calculate how much error there is for M registers, the equation is: expectedError = 1.04 / sqrt(M)

To calculate how many registers you need to achieve a specific expected error, the equation is: M = 676 / (625 * expectedError^2)

In those equations, an expectedError of 0.03 would mean 3%.

Check out the table below to get an idea of accuracy vs size.

Note that since we use bits from our hash to do register selection, that our number of registers is a power of 2.

Register Bits	Register Count	Error
0	1	104%
1	2	73.5%
2	4	52%
3	8	36.7%
4	16	26%
5	32	18.3%
6	64	13%
7	128	9%
8	256	6.5%
9	512	4.6%
10	1024	3.2%
11	2048	2.2%
12	4096	1.6%

Here is a graph showing how number of bits used affects error. Bits used is the x axis, and expected error is the y axis.

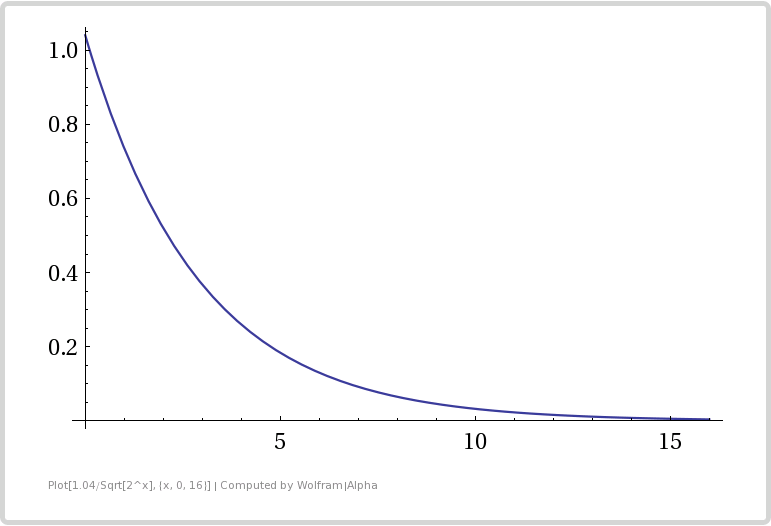
From the table and the graph you can see that adding bits (registers) gives diminishing returns in error reduction. It’s especially diminishing because whenever we add another bit, we double our storage size (double the number of registers we use).

This shows us that this algorithm is great at counting a large number of uniques, since one byte per counter can count up to about 2^256 (2^2^8) uniques, but it isn’t super great at getting a low error rate. If you are ok with about 2% accuracy, the storage space needed is pretty small though!

Remember the claim at the top of this post?

“…the new algorithm makes it possible to estimate cardinalities well beyond 10^9 with a typical accuracy of 2% while using a memory of only 1.5 kilobytes”

Looking at the bits used / error table, you can see 11 bits, or 2048 registers, gives just a little over 2% accuracy.

If you are using 32 bits of hash to look for runs of zeros, you can use 6 bit registers to store the longest run seen, if you want to waste a bit to be able to store 0-32 instead of just 0-31.

So, 2048 registers * 6 bits = 12288 bits of register storage needed. That is 1536 bytes, or exactly 1.5KB.

You could count up to ~4 billion uniques (2^32) with that configuration, but error increases as you get closer to that limit, so I think that’s why they limited their statement to counting ~1 billion uniques (10^9).

Estimating Counts

The math behind the count estimation is a bit complex (check the paper in the links section for more info!) but part of how it works is it uses the harmonic mean to average the data from the registers together. Since there is randomness involved, and differences in our run lengths means being off by exponential amounts, the harmonic mean is great at filtering out large outliers due to the random fluctuations. Fluctuation to the “too small” end won’t matter too much since it will be over-written by other values since we are storing the maximum value seen. Fluctuations to the “too large” end are mitigated with harmonic mean.

Here’s some pseudo code for estimating the count. Note that we are storing the position of the first 1 in the registers, not storing the run length of zeros. That’s an important distinction because it means the number is 1 higher than it would be otherwise, which if you get it wrong makes your estimation half as large as it should be. It also means that you know if you see a zero register, that it is uninitialized and hasn’t seen a value yet.

Alpha = 0.7213 / (1 + 1.079 / NumRegisters)
Sum = 0
for i = 0 to NumRegisters
  Sum = Sum + pow(2, -Register[i])

Estimation = Alpha * NumRegisters^2 / Sum

// do small range correction
if Estimation < 5 / 2 * NumRegisters
{
  if NumEmptyRegisters > 0
    Estimation = NumRegisters * ln(NumRegisters / NumEmptyRegisters)
}
// do large range correction
else if Estimation > 2^32 / 30
{
  Estimation = -2^32 * ln(1 - Estimation/ 2^32);
}

Small range correction is there because when not enough registers have been filled in (they haven’t gotten any data yet), the normal algorithm path has expected error greater than 1.04. Large range correction is there for the same reason, but on the high end side, when the registers are saturated.

Set Operations

You can do set operations on hyperloglog objects so long as they use the same number of registers, same sized registers, and same hashing algorithm.

There’s a link in the links section at the end of this post that shows you how to resize the number of registers so that you can do set operations on HLL objects that have different numbers of registers.

Union

Taking a union of two HLL objects is actually really simple.

If you have two HLL objects A and B, that you want to union to get C, all you do is take the maximum bucket value from A and B and store it in C. Check out this pseudocode to see what i mean:

for i = 0 to NumRegisters
  C.Register[i] = Max(A.Register[i], B.Register[i])

The neat thing about doing this union is that it is LOSSLESS and doesn’t introduce any new error. Doing a union of two HLL objects is just the same as if you had a third HLL object that processed all the same objects that A and B both processed.

Intersection

To do an intersection is a tiny bit trickier, but not by much. We have to use what is called the Inclusion-Exclusion Principle (check links section for more info).

Using that principle, we can estimate the count of how many items are in the intersection, but we can’t get a HLL object representing the intersection of the two objects unfortunately.

The formula is this:

Count(Intersection(A,B)) = Count(A) + Count(B) – Count(Union(A,B))

And here’s some more pseudocode to show you how to do it:

C = Union(A,B)
IntersectionCountEstimate = A.CountEstimate() + B.CountEstimate() - C.CountEstimate()

Pretty simple eh?

At the beginning I mentioned that KMV was actually better at intersections than HyperLogLog. The reason for that is because with KMV, you have a small, random sample range from both objects, and you can do an intersection between those two ranges and get your result.

KMV really starts to shine when you need to do an intersection between more than 2 or 3 lists, because using the inclusion-exclusion principle causes a combinatorial explosion, while the KMV intersection easily extends for N sets.

Jaccard Index

There’s no special trick to calculating the Jaccard Index, as per usual it’s just:

JaccardIndex = Count(Intersection(A,B)) / Count(Union(A,B))

Which will give you a value from 0 to 1 indicating how similar the two sets A and B are, where 1 is totally the same, and 0 is completely different. In the case of HLL, this is an estimated Jaccard Index of course, not the actual value!

Contains Percent

I was noticing in runs of the sample code below that while the union operation had pretty decent error levels, the intersection operation had not so great error levels and thus the Jaccard Index wasn’t very accurate either. This is mostly due to the fact that the intersection levels were pretty small, so if you had +1 or -1, that came out to be a large percentage of the actual value.

Despite having a reasonable explanation that diminished the actual impact of the “high error levels”, I wanted to see if I could come up with a different similarity metric and see how the error rate was on it.

What I came up with was a “Contains Percent”, which is the percentage of how many items in A are contained in B. You calculate it like this:

ContainsPercent = Count(Intersection(A,B)) / Count(A)

Since it uses the intersection value (that is not so accurate), it didn’t give great results, but I wanted to mention it because it actually is a completely different measurement than Jaccard Index with different meaning. All of the items in A could be in B, which would give it a “ContainsPercent” of 1.0, but B may have 10 times as many items that don’t appear in A, which would make the Jaccard Index very low.

In some cases, you may want to use the information that the Jaccard Index represents to make decisions, and in other cases you may want this “Contains Percent” metric, or maybe even something else.

It’s a bit subtle, but it’s good to think about what it is that you are actually looking for if using these things in actual production code (:

Estimating Set Membership

So, HLL is NOT a bloom filter, but can it still be used like one?

The answer is yes, but I don’t have a whole lot of information about the formal accuracy of that.

Basically how you’d do this is create a temporary HLL object, make it store the single item you want to check the other HLL for set membership of, and then you’d do an estimated intersection count between the two HLL objects.

As crazy as it sounds, it looks like redis exposes this functionality and says it is pretty accurate (for however many registers they used anyways), which is pretty neat:
Redis: PFCOUNT

Dot Product

The dot product between two sets (or multi sets – where you have a count associated with each item) can be really useful to help gauge the similarity between the two sets.

You can do a dot product operation between two HLL objects too. If you think about it, getting the dot product between two HLL objects is the same as getting the estimated count of the intersection between those two objects.

Example Code

Here is some example code in C++ that allows you to do HyperLogLog. It includes only standard include files so has no dependencies and is in a single file for convenience.

I use a hash called MurmurHash3 to generate 128 bits of hash, 32 bits of which are used to generate the register index, and the remaining 96 bits are used for looking at runs of zeros.

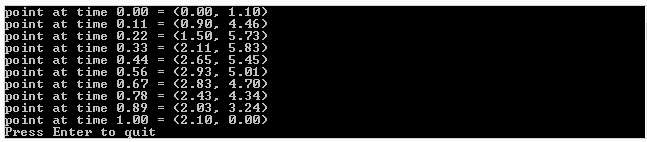
Below the code is the output of a run of this program

#include <array>
#include <string>
#include <assert.h>
#include <unordered_set>
#include <stdint.h>
#include <memory>
 
// microsoft only, for _BitScanForward to quickly find the index of the first 1 bit
// Use clz in gcc
#include <intrin.h>
 
//=====================================================================================================
// MurmurHash3
//=====================================================================================================
 
// from https://code.google.com/p/smhasher/source/browse/trunk/MurmurHash3.cpp
// note that this 128 bit MurmurHash3 is optimized for x86.  There is a version at the above link
// optimized for x64 as well, but it gives different output for the same input.
 
#define ROTL32(x,y)     _rotl(x,y)
 
inline uint32_t getblock32 (const uint32_t * p, int i)
{
    return p[i];
}
 
inline uint32_t fmix32 (uint32_t h)
{
    h ^= h >> 16;
    h *= 0x85ebca6b;
    h ^= h >> 13;
    h *= 0xc2b2ae35;
    h ^= h >> 16;
 
    return h;
}
 
void MurmurHash3_x86_128 (const void * key, const int len,
    uint32_t seed, std::array<uint32_t, 4> & out)
{
    const uint8_t * data = (const uint8_t*)key;
    const int nblocks = len / 16;
 
    uint32_t h1 = seed;
    uint32_t h2 = seed;
    uint32_t h3 = seed;
    uint32_t h4 = seed;
 
    const uint32_t c1 = 0x239b961b;
    const uint32_t c2 = 0xab0e9789;
    const uint32_t c3 = 0x38b34ae5;
    const uint32_t c4 = 0xa1e38b93;
 
    //----------
    // body
 
    const uint32_t * blocks = (const uint32_t *)(data + nblocks * 16);
 
    for (int i = -nblocks; i; i++)
    {
        uint32_t k1 = getblock32(blocks, i * 4 + 0);
        uint32_t k2 = getblock32(blocks, i * 4 + 1);
        uint32_t k3 = getblock32(blocks, i * 4 + 2);
        uint32_t k4 = getblock32(blocks, i * 4 + 3);
 
        k1 *= c1; k1 = ROTL32(k1, 15); k1 *= c2; h1 ^= k1;
 
        h1 = ROTL32(h1, 19); h1 += h2; h1 = h1 * 5 + 0x561ccd1b;
 
        k2 *= c2; k2 = ROTL32(k2, 16); k2 *= c3; h2 ^= k2;
 
        h2 = ROTL32(h2, 17); h2 += h3; h2 = h2 * 5 + 0x0bcaa747;
 
        k3 *= c3; k3 = ROTL32(k3, 17); k3 *= c4; h3 ^= k3;
 
        h3 = ROTL32(h3, 15); h3 += h4; h3 = h3 * 5 + 0x96cd1c35;
 
        k4 *= c4; k4 = ROTL32(k4, 18); k4 *= c1; h4 ^= k4;
 
        h4 = ROTL32(h4, 13); h4 += h1; h4 = h4 * 5 + 0x32ac3b17;
    }
 
    //----------
    // tail
 
    const uint8_t * tail = (const uint8_t*)(data + nblocks * 16);
 
    uint32_t k1 = 0;
    uint32_t k2 = 0;
    uint32_t k3 = 0;
    uint32_t k4 = 0;
 
    switch (len & 15)
    {
    case 15: k4 ^= tail[14] << 16;
    case 14: k4 ^= tail[13] << 8;
    case 13: k4 ^= tail[12] << 0;
        k4 *= c4; k4 = ROTL32(k4, 18); k4 *= c1; h4 ^= k4;
 
    case 12: k3 ^= tail[11] << 24;
    case 11: k3 ^= tail[10] << 16;
    case 10: k3 ^= tail[9] << 8;
    case  9: k3 ^= tail[8] << 0;
        k3 *= c3; k3 = ROTL32(k3, 17); k3 *= c4; h3 ^= k3;
 
    case  8: k2 ^= tail[7] << 24;
    case  7: k2 ^= tail[6] << 16;
    case  6: k2 ^= tail[5] << 8;
    case  5: k2 ^= tail[4] << 0;
        k2 *= c2; k2 = ROTL32(k2, 16); k2 *= c3; h2 ^= k2;
 
    case  4: k1 ^= tail[3] << 24;
    case  3: k1 ^= tail[2] << 16;
    case  2: k1 ^= tail[1] << 8;
    case  1: k1 ^= tail[0] << 0;
        k1 *= c1; k1 = ROTL32(k1, 15); k1 *= c2; h1 ^= k1;
    };
 
    //----------
    // finalization
 
    h1 ^= len; h2 ^= len; h3 ^= len; h4 ^= len;
 
    h1 += h2; h1 += h3; h1 += h4;
    h2 += h1; h3 += h1; h4 += h1;
 
    h1 = fmix32(h1);
    h2 = fmix32(h2);
    h3 = fmix32(h3);
    h4 = fmix32(h4);
 
    h1 += h2; h1 += h3; h1 += h4;
    h2 += h1; h3 += h1; h4 += h1;
 
    out[0] = h1;
    out[1] = h2;
    out[2] = h3;
    out[3] = h4;
}
 
struct SMurmurHash3
{
    std::array<uint32_t, 4> HashBytes (const void *key, size_t len)
    {
        // use a random 32 bit number as the seed (salt) of the hash.
        // Gotten from random.org
        // https://www.random.org/cgi-bin/randbyte?nbytes=4&format=h
        static const uint32_t c_seed = 0x2e715b3d;
 
        // MurmurHash3 doesn't do well with small input sizes, so if the input is too small,
        // make it longer in a way that hopefully doesn't cause likely collisions.
        // "the" hashed before the fix (notice the last 3 are the same)
        //  0x45930d0e
        //  0xfc76ee5b
        //  0xfc76ee5b
        //  0xfc76ee5b
        // and after the fix:
        //  0x70220da0
        //  0xe7d0664a
        //  0xb4e4d832
        //  0x25940640
        std::array<uint32_t, 4> ret;
        static const size_t c_minLen = 16;
        if (len < c_minLen)
        {
            unsigned char buffer[c_minLen];
 
            for (size_t i = 0; i < len; ++i)
                buffer[i] = ((unsigned char*)key)[i];
 
            for (size_t i = len; i < c_minLen; ++i)
                buffer[i] = buffer[i%len] + i;
 
            MurmurHash3_x86_128(buffer, c_minLen, c_seed, ret);
        }
        else
        {
            MurmurHash3_x86_128(key, len, c_seed, ret);
        }
 
        return ret;
    }
 
    template <typename T>
    std::array<uint32_t, 4> operator() (const T &object);
 
    template <>
    std::array<uint32_t, 4> operator() <std::string> (const std::string &object)
    {
        return HashBytes(object.c_str(), object.length());
    }
 
    // NOTE: if you need to hash other object types, just make your own template specialization here
};
 
//=====================================================================================================
// The CHyperLogLog class
//=====================================================================================================
//
// TKEY is the type of objects to keep track of
// NUMREGISTERBITS is how many bits of the hash are used to index into registers.  It also controls
//   how many registers there are since that count is 2^NUMREGISTERBITS
// HASHER controls how the keys are hashed
//
template <typename TKEY, size_t NUMREGISTERBITS, typename HASHER>
class CHyperLogLog
{
public:
    CHyperLogLog()
        : m_counts{} // init counts to zero
    { }
 
    // friends
    template <typename TKEY, size_t NUMREGISTERBITS, typename HASHER>
    friend float UnionCountEstimate (const CHyperLogLog<TKEY, NUMREGISTERBITS, HASHER>& A, const CHyperLogLog<TKEY, NUMREGISTERBITS, HASHER>& B);
 
    // constants
    static const size_t c_numRegisters = 1 << NUMREGISTERBITS;
    static const size_t c_registerMask = (c_numRegisters - 1);
 
    // interface
    void AddItem (const TKEY& item)
    {
        // because 2^32 does not fit in 32 bits
        static_assert(NUMREGISTERBITS < 32, "CHyperLogLog must use fewer than 32 register bits");
 
        // make as many hashed bits as we need
        std::array<uint32_t, 4> hash = HASHER()(item);
 
        // use the highest 32 bits for getting our register index
        unsigned int registerIndex = hash[3] & c_registerMask;
 
        // use the other 96 bits as our "unique number" corresponding to our object.  Note that we
        // don't use the high 32 bits that we've already used for the register index because that
        // would bias our results.  Certain values seen would ONLY get tracked by specific registers.
        // That's ok though that we are only using 96 bits because that is still an astronomically large
        // value.  Most HyperLogLog implementations use only 32 bits, while google uses 64 bits.  We are
        // doing even larger with 96 bits.
        // 2^(bits) = how many unique items you can track.
        //
        // 2^32  = 4 billion <--- what most people use
        // 2^64  = 18 billion billion <--- what google uses
        // 2^96  = 79 billion billion billion <--- what we are using
        // 2^128 = 340 billion billion billion billion <--- way huger than anyone needs. Beyond astronomical.
 
        // Figure out where the highest 1 bit is
        unsigned long bitSet = 0;
        if (_BitScanForward(&bitSet, hash[0]))
            bitSet += 1;
        else if (_BitScanForward(&bitSet, hash[1]))
            bitSet += 32 + 1;
        else if (_BitScanForward(&bitSet, hash[2]))
            bitSet += 64 + 1;
 
        // store the highest seen value for that register
        assert(bitSet < 256);
        unsigned char value = (unsigned char)bitSet;
        if (m_counts[registerIndex] < value)
            m_counts[registerIndex] = value;
 
    }
 
    unsigned int EmptyRegisterCount () const
    {
        unsigned int ret = 0;
        std::for_each(m_counts.begin(), m_counts.end(), [&] (unsigned char count) {
            if (count == 0)
                ret++;
        });
        return ret;
    }
 
    float GetCountEstimation () const
    {
        // calculate dv estimate
        const float c_alpha = 0.7213f / (1.0f + 1.079f / c_numRegisters);
        float sum = 0.0f;
        std::for_each(m_counts.begin(), m_counts.end(), [&](unsigned char count) {
            sum += std::pow(2.0f, -(float)count);
        });
 
        float dv_est = c_alpha * ((float)c_numRegisters / sum) * (float)c_numRegisters;
 
        // small range correction
        if (dv_est < 5.0f / 2.0f * (float)c_numRegisters)
        {
            // if no empty registers, use the estimate we already have
            unsigned int emptyRegisters = EmptyRegisterCount();
            if (emptyRegisters == 0)
                return dv_est;
 
            // balls and bins correction
            return (float)c_numRegisters * log((float)c_numRegisters / (float)emptyRegisters);
        }
 
        // large range correction
        if (dv_est > 143165576.533f) // 2^32 / 30
            return -pow(2.0f, 32.0f) * log(1.0f - dv_est / pow(2.0f, 32.0f));
 
        return dv_est;
    }
 
private:
    std::array<unsigned char, c_numRegisters> m_counts;
};
 
// there seem to be numerical problems when using 26 bits or larger worth of registers
typedef CHyperLogLog<std::string, 10, SMurmurHash3> TCounterEstimated;
typedef std::unordered_set<std::string> TCounterActual;
 
//=====================================================================================================
// Set Operations
//=====================================================================================================
 
template <typename TKEY, size_t NUMREGISTERBITS, typename HASHER>
float UnionCountEstimate (
    const CHyperLogLog<TKEY, NUMREGISTERBITS, HASHER>& A,
    const CHyperLogLog<TKEY, NUMREGISTERBITS, HASHER>& B)
{
    // dynamically allocate our hyperloglog object to not bust the stack if you are using a lot of registers.
    std::unique_ptr<CHyperLogLog<TKEY, NUMREGISTERBITS, HASHER>> temp =
        std::make_unique<CHyperLogLog<TKEY, NUMREGISTERBITS, HASHER>>();
 
    // To make a union between two hyperloglog objects that have the same number of registers and use
    // the same hash, just take the maximum of each register between the two objects.  This operation is
    // "lossless" in that you end up with the same registers as if you actually had another object
    // that tracked the items each individual object tracked.
    for (size_t i = 0; i < (*temp).c_numRegisters; ++i)
        (*temp).m_counts[i] = std::max(A.m_counts[i], B.m_counts[i]);
    return (*temp).GetCountEstimation();
}
 
template <typename TKEY, size_t NUMREGISTERBITS, typename HASHER>
float IntersectionCountEstimate (
    const CHyperLogLog<TKEY, NUMREGISTERBITS, HASHER>& A,
    const CHyperLogLog<TKEY, NUMREGISTERBITS, HASHER>& B)
{
    // We have to use the inclusion-exclusion principle to get an intersection estimate
    // count(Intersection(A,B)) = (count(A) + count(B)) - count(Union(A,B))
    // http://en.wikipedia.org/wiki/Inclusion%E2%80%93exclusion_principle
 
    return (A.GetCountEstimation() + B.GetCountEstimation()) - UnionCountEstimate(A, B);
}
 
float UnionCountActual (const TCounterActual& A, const TCounterActual& B)
{
    TCounterActual temp;
    std::for_each(A.begin(), A.end(), [&] (const TCounterActual::key_type &s){temp.insert(s);});
    std::for_each(B.begin(), B.end(), [&] (const TCounterActual::key_type &s){temp.insert(s);});
    return (float)temp.size();
}
 
float IntersectionCountActual (const TCounterActual& A, const TCounterActual& B)
{
    float ret = 0;
    std::for_each(A.begin(), A.end(), [&](const TCounterActual::key_type &s)
    {
        if (B.find(s) != B.end())
            ++ret;
    });
    return ret;
}
 
//=====================================================================================================
// Error Calculations
//=====================================================================================================
 
float ExpectedError (size_t numRegisters)
{
    return 1.04f / ((float)(sqrt((float)numRegisters)));
}
 
float IdealRegisterCount (float expectedError)
{
    return 676.0f / (625.0f * expectedError * expectedError);
}
 
//=====================================================================================================
// Driver Program
//=====================================================================================================
 
template <typename L>
void ForEachWord(const std::string &source, L& lambda)
{
    size_t prev = 0;
    size_t next = 0;
 
    while ((next = source.find_first_of(" ,.-":n", prev)) != std::string::npos)
    {
        if ((next - prev != 0))
        {
            std::string word = source.substr(prev, next - prev);
            std::transform(word.begin(), word.end(), word.begin(), ::tolower);
            lambda(word);
        }
        prev = next + 1;
    }
 
    if (prev < source.size())
    {
        std::string word = source.substr(prev);
        std::transform(word.begin(), word.end(), word.begin(), ::tolower);
        lambda(word);
    }
}
 
template <typename T>
const char *CalculateError (const T&estimate, const T&actual)
{
    float error = 100.0f * ((float)estimate - (float)actual) / (float)actual;
    if (std::isnan(error) || std::isinf(error))
        return "undef";
 
    // bad practice to return a static local string, dont do this in production code!
    static char ret[256];
    sprintf_s(ret, sizeof(ret), "%0.2f%%", error);
    return ret;
}
 
char *BytesToHumanReadable (size_t bytes)
{
    // bad practice to return a static local string, dont do this in production code!
    static char ret[256];
    if (bytes >= 1024 * 1024 * 1024)
        sprintf_s(ret, sizeof(ret), "%0.2fGB", ((float)bytes) / (1024.0f*1024.0f*1024.0f));
    else if (bytes >= 1024 * 1024)
        sprintf_s(ret, sizeof(ret), "%0.2fMB", ((float)bytes) / (1024.0f*1024.0f));
    else if (bytes >= 1024)
        sprintf_s(ret, sizeof(ret), "%0.2fKB", ((float)bytes) / (1024.0f));
    else
        sprintf_s(ret, sizeof(ret), "%u Bytes", bytes);
    return ret;
}
 
void WaitForEnter()
{
    printf("nPress Enter to quit");
    fflush(stdin);
    getchar();
}
 
// These one paragraph stories are from http://birdisabsurd.blogspot.com/p/one-paragraph-stories.html
 
// The Dino Doc : http://birdisabsurd.blogspot.com/2011/11/dino-doc.html (97 words)
const char *g_storyA =
"The Dino Doc:n"
"Everything had gone according to plan, up 'til this moment. His design team "
"had done their job flawlessly, and the machine, still thrumming behind him, "
"a thing of another age, was settled on a bed of prehistoric moss. They'd "
"done it. But now, beyond the protection of the pod and facing an enormous "
"tyrannosaurus rex with dripping jaws, Professor Cho reflected that, had he "
"known of the dinosaur's presence, he wouldn't have left the Chronoculator - "
"and he certainly wouldn't have chosen "Stayin' Alive", by The Beegees, as "
"his dying soundtrack. Curse his MP3 player";
 
// The Robot: http://birdisabsurd.blogspot.com/2011/12/robot.html (121 words)
const char *g_storyB =
"The Robot:n"
"The engineer watched his robot working, admiring its sense of purpose.It knew "
"what it was, and what it had to do.It was designed to lift crates at one end "
"of the warehouse and take them to the opposite end.It would always do this, "
"never once complaining about its place in the world.It would never have to "
"agonize over its identity, never spend empty nights wondering if it had been "
"justified dropping a promising and soul - fulfilling music career just to "
"collect a bigger paycheck.And, watching his robot, the engineer decided that "
"the next big revolution in the robotics industry would be programming "
"automatons with a capacity for self - doubt.The engineer needed some company.";
 
// The Internet: http://birdisabsurd.blogspot.com/2011/11/internet.html (127 words)
const char *g_storyC =
"The Internet:n"
"One day, Sandra Krewsky lost her mind.Nobody now knows why, but it happened - "
"and when it did, Sandra decided to look at every page on the Internet, "
"insisting that she wouldn't eat, drink, sleep or even use the washroom until "
"the job was done. Traps set in her house stalled worried family members, and by "
"the time they trounced the alligator guarding her bedroom door - it managed to "
"snap her neighbour's finger clean off before going down - Sandra was already "
"lost… though the look of despair carved in her waxen features, and the cat "
"video running repeat on her flickering computer screen, told them everything "
"they needed to know.She'd seen too much. She'd learned that the Internet "
"played for keeps.";
 
int main (int argc, char **argv)
{
    // show basic info regarding memory usage, precision, etc
    printf("For %u registers at 1 byte per register, the expected error is %0.2f%%.n",
        TCounterEstimated::c_numRegisters,
        100.0f * ExpectedError(TCounterEstimated::c_numRegisters)
    );
    printf("Memory Usage = %s per HyperLogLog object.n", BytesToHumanReadable(TCounterEstimated::c_numRegisters));
    static const float c_expectedError = 0.03f;
    printf("For expected error of %0.2f%%, you should use %0.2f registers.nn",
        100.0f*c_expectedError,
        IdealRegisterCount(c_expectedError)
    );
 
    // populate our data structures
    // dynamically allocate estimate so we don't bust the stack if we have a large number of registers
    std::unique_ptr<TCounterEstimated> estimateTotal = std::make_unique<TCounterEstimated>();
    std::unique_ptr<TCounterEstimated> estimateA = std::make_unique<TCounterEstimated>();
    std::unique_ptr<TCounterEstimated> estimateB = std::make_unique<TCounterEstimated>();
    std::unique_ptr<TCounterEstimated> estimateC = std::make_unique<TCounterEstimated>();
    TCounterActual actualTotal;
    TCounterActual actualA;
    TCounterActual actualB;
    TCounterActual actualC;
    {
        auto f = [&](const std::string &word)
        {
            estimateTotal->AddItem(word);
            actualTotal.insert(word);
        };
 
        auto fA = [&](const std::string &word)
        {
            estimateA->AddItem(word);
            actualA.insert(word);
            f(word);
        };
 
        auto fB = [&](const std::string &word)
        {
            estimateB->AddItem(word);
            actualB.insert(word);
            f(word);
        };
 
        auto fC = [&](const std::string &word)
        {
            estimateC->AddItem(word);
            actualC.insert(word);
            f(word);
        };
 
        ForEachWord(g_storyA, fA);
        ForEachWord(g_storyB, fB);
        ForEachWord(g_storyC, fC);
    }
 
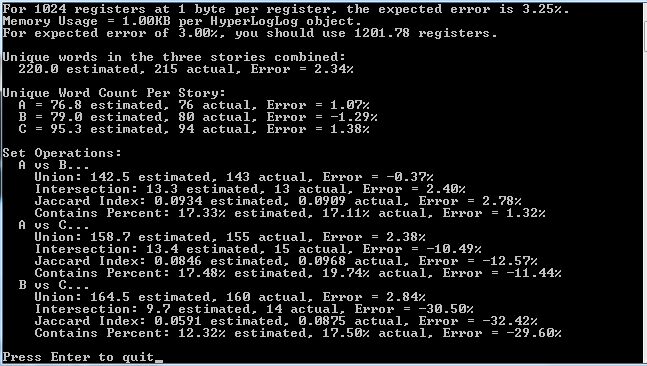
    // Show unique word counts for the three combined stories
    {
        float estimateCount = estimateTotal->GetCountEstimation();
        float actualCount = (float)actualTotal.size();
        printf("Unique words in the three stories combined:n");
        printf("  %0.1f estimated, %.0f actual, Error = %snn",
            estimateCount,
            actualCount,
            CalculateError(estimateCount, actualCount)
        );
    }
     
    // show unique word counts per story
    {
        printf("Unique Word Count Per Story:n");
        auto g = [](const char *name, const TCounterEstimated &estimate, const TCounterActual &actual)
        {
            float estimateCount = estimate.GetCountEstimation();
            float actualCount = (float)actual.size();
            printf("  %s = %0.1f estimated, %.0f actual, Error = %sn",
                name,
                estimateCount,
                actualCount,
                CalculateError(estimateCount, actualCount)
            );
        };
         
        g("A", *estimateA, actualA);
        g("B", *estimateB, actualB);
        g("C", *estimateC, actualC);
    }
 
    // Set Operations
    {
        printf("nSet Operations:n");
 
        auto f = [] (
            const char *name1,
            const TCounterEstimated &estimate1,
            const TCounterActual &actual1,
            const char *name2,
            const TCounterEstimated &estimate2,
            const TCounterActual &actual2
        )
        {
            printf("  %s vs %s...n", name1, name2);
 
            // union
            float estimateUnionCount = UnionCountEstimate(estimate1, estimate2);
            float actualUnionCount = UnionCountActual(actual1, actual2);
            printf("    Union: %0.1f estimated, %.0f actual, Error = %sn",
                estimateUnionCount,
                actualUnionCount,
                CalculateError(estimateUnionCount, actualUnionCount)
            );
 
            // intersection
            float estimateIntersectionCount = IntersectionCountEstimate(estimate1, estimate2);
            float actualIntersectionCount = IntersectionCountActual(actual1, actual2);
            printf("    Intersection: %0.1f estimated, %.0f actual, Error = %sn",
                estimateIntersectionCount,
                actualIntersectionCount,
                CalculateError(estimateIntersectionCount, actualIntersectionCount)
            );
 
            // jaccard index
            float estimateJaccard = estimateIntersectionCount / estimateUnionCount;
            float actualJaccard = actualIntersectionCount / actualUnionCount;
            printf("    Jaccard Index: %0.4f estimated, %.4f actual, Error = %sn",
                estimateJaccard,
                actualJaccard,
                CalculateError(estimateJaccard, actualJaccard)
            );
 
            // Contains Percent.
            // What percentage of items in A are also in B?
            float estimateSim = estimateIntersectionCount / estimate1.GetCountEstimation();
            float actualSim = actualIntersectionCount / actual1.size();
            printf("    Contains Percent: %0.2f%% estimated, %0.2f%% actual, Error = %sn",
                100.0f*estimateSim,
                100.0f*actualSim,
                CalculateError(estimateSim, actualSim)
            );
        };
 
        f("A", *estimateA, actualA, "B", *estimateB, actualB);
        f("A", *estimateA, actualA, "C", *estimateC, actualC);
        f("B", *estimateB, actualB, "C", *estimateC, actualC);
    }
 
    WaitForEnter();
    return 0;
}

Here is the output of the above program:

Want More?

As per usual, the rabbit hole goes far deeper than what I’ve shown. Check out the links below to go deeper!

HyperLogLog Research Paper
Combining HLL and KMV to Get The Best of Both
Doubling the Count of HLL Registers on the Fly
Set Operations on HLLs of Different Sizes
Interactive HyperLogLog Demo
Interactive HyperLogLog Union Demo
HyperLogLog++ Research Paper
HyperLogLog++ Analyzed
Wikipedia: Inclusion Exclusion Principle
Coin Flipping
Wikipedia: MurmurHash3
MurmurHash3 C++ Source Code